GLFSR Source: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Bigwillis234 (talk | contribs) No edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Block Docs]] | [[Category:Block Docs]] | ||
Galois LFSR pseudo-random source generating float outputs -1.0 - 1.0. | Galois LFSR pseudo-random source generating float outputs -1.0 - 1.0. Generates a maximal length sequence of length 2^degree-1. | ||
== Parameters == | == Parameters == | ||
| Line 11: | Line 12: | ||
; Mask | ; Mask | ||
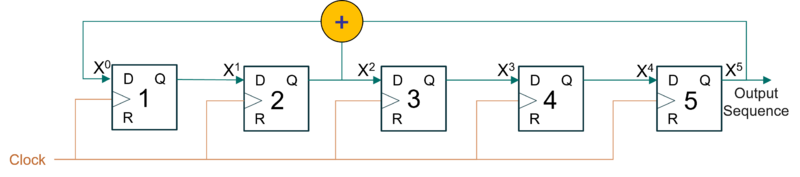
: Allows a user-defined bit mask for indexes of the shift register to feed back. | : Allows a user-defined bit mask for indexes of the shift register to feed back. For example the two fifth-order primitive polynomials, p(x) = x^5 + x^4 + x^3 + x^2 + 1 and p(x) = x^5 + x^2 + 1, will create m-sequences of length 2^n-1 where n is the degree. The mask is in byte format specifying the taps. The "one" in the polynomial does not correspond to a tap – it corresponds to the input to the first bit and is excluded from the mask. So the polynomials would be entered into the mask as 0x1E and 0x12 respectively. Note that these are integers, so after they are enter in the GNURadio block they will show as decimal 30 and 18, respectively. | ||
[[File:FifthOrder.png|800px|A Fifth Order LFSR corresponding to p(x)= (5,2,0).]] | |||
; Seed | ; Seed | ||
| Line 18: | Line 21: | ||
== Example Flowgraph == | == Example Flowgraph == | ||
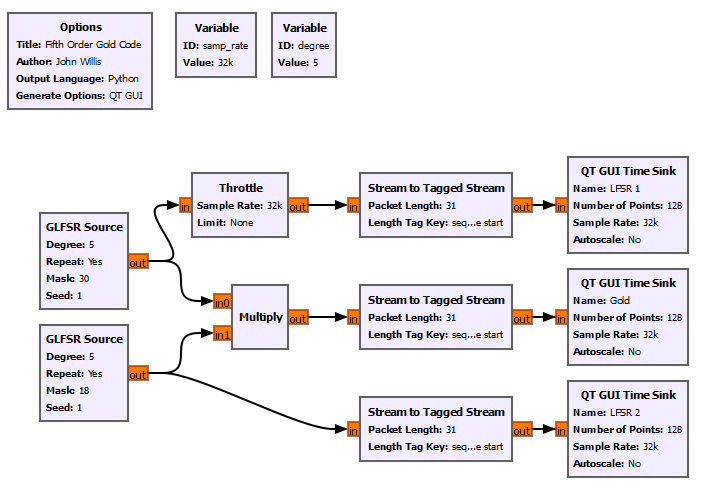
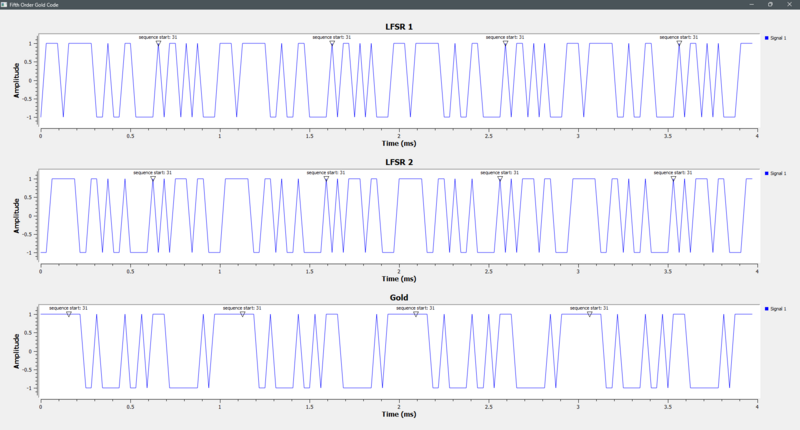
Example of the two polynomials, p(x) = x^5 + x^4 + x^3 + x^2 + 1 and p(x) = x^5 + x^2 + 1, to create a Gold Code Sequence. | |||
[[File:FifthOrderGoldGenerator.png|800px|A Fifth Order LFSR Gold Code Using GFLSR.]] | |||
[[File:FifthOrderGoldGeneratorOutput.png|800px|A Fifth Order LFSR Gold Code Using GFLSR.]] | |||
== Source Files == | == Source Files == | ||
; C++ | ; C++ files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-digital/lib/glfsr_source_b_impl.cc glfsr_source_b_impl.cc] | ||
: [https://github.com/gnuradio/gnuradio/blob/main/gr-digital/lib/glfsr.cc glfsr.cc] | |||
; Header files | ; Header files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-digital/lib/glfsr_source_b_impl.h glfsr_source_b_impl.h] | ||
; Public header files | ; Public header files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-digital/include/gnuradio/digital/glfsr.h glfsr.h] | ||
; Block definition | ; Block definition | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-digital/grc/digital_glfsr_source_x.block.yml digital_glfsr_source_x.block.yml] | ||
Latest revision as of 20:18, 21 August 2024
Galois LFSR pseudo-random source generating float outputs -1.0 - 1.0. Generates a maximal length sequence of length 2^degree-1.
Parameters
- Degree
- Degree of shift register must be in [1, 32]. If mask is 0, the degree determines a default mask (see digital_impl_glfsr.cc for the mapping).
- Repeat
- Set to repeat sequence.
- Mask
- Allows a user-defined bit mask for indexes of the shift register to feed back. For example the two fifth-order primitive polynomials, p(x) = x^5 + x^4 + x^3 + x^2 + 1 and p(x) = x^5 + x^2 + 1, will create m-sequences of length 2^n-1 where n is the degree. The mask is in byte format specifying the taps. The "one" in the polynomial does not correspond to a tap – it corresponds to the input to the first bit and is excluded from the mask. So the polynomials would be entered into the mask as 0x1E and 0x12 respectively. Note that these are integers, so after they are enter in the GNURadio block they will show as decimal 30 and 18, respectively.
- Seed
- Initial setting for values in shift register.
Example Flowgraph
Example of the two polynomials, p(x) = x^5 + x^4 + x^3 + x^2 + 1 and p(x) = x^5 + x^2 + 1, to create a Gold Code Sequence.
Source Files
- C++ files
- Header files
- glfsr_source_b_impl.h
- Public header files
- glfsr.h
- Block definition
- digital_glfsr_source_x.block.yml