FM Preemphasis: Difference between revisions
(Created page with "Category:Block Docs Category:Stub Docs This is the template for the "Page-per-block Docs". This first section should describe what the block...") |
(space missing) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Block Docs]] | [[Category:Block Docs]] | ||
An analog preemphasis filter, that flattens out again at the high end: | |||
C | |||
+-----||------+ | |||
| | | |||
o------+ +-----+--------o | |||
| R1 | | | |||
+----/\/\/\/--+ \ | |||
/ | |||
\ R2 | |||
/ | |||
\ | |||
| | |||
o--------------------------+--------o | |||
(This fine ASCII rendition is based on Figure 5-15 | |||
in "Digital and Analog Communication Systems", Leon W. Couch II) | |||
Has this transfer function: | |||
1 | |||
s + --- | |||
R1C | |||
H(s) = ------------------ | |||
1 R1 | |||
s + --- (1 + --) | |||
R1C R2 | |||
It has a corner due to the numerator, where the rise starts, at | |||
|Hn(j w_cl)|^2 = 2*|Hn(0)|^2 => s = j w_cl = j (1/(R1C)) | |||
It has a corner due to the denominator, where it levels off again, at | |||
|Hn(j w_ch)|^2 = 1/2*|Hd(0)|^2 => s = j w_ch = j (1/(R1C) * (1 + R1/R2)) | |||
Historically, the corner frequency of analog audio preemphasis filters | |||
been specified by the R1C time constant used, called tau. | |||
So | |||
w_cl = 1/tau = 1/R1C; f_cl = 1/(2*pi*tau) = 1/(2*pi*R1*C) | |||
w_ch = 1/tau2 = (1+R1/R2)/R1C; f_ch = 1/(2*pi*tau2) = (1+R1/R2)/(2*pi*R1*C) | |||
and note f_ch = f_cl * (1 + R1/R2). | |||
For broadcast FM audio, tau is 75us in the United States and 50us in Europe. | |||
f_ch should be higher than our digital audio bandwidth. | |||
The Bode plot looks like this: | |||
/---------------- | |||
/ | |||
/ <-- slope = 20dB/decade | |||
/ | |||
-------------/ | |||
f_cl f_ch | |||
In specifying tau for this digital preemphasis filter, tau specifies the *digital* corner frequency, w_cl, desired. | |||
The digital preemphasis filter design below, uses the"bilinear transformation" method of designing digital filters: | |||
1. Convert digital specifications into the analog domain, by prewarping digital frequency specifications into analog frequencies. | |||
w_a = (2/T)tan(wT/2) | |||
2. Use an analog filter design technique to design the filter. | |||
3. Use the bilinear transformation to convert the analog filter design to a digital filter design. | |||
H(z) = H(s)| | |||
s = (2/T)(1-z^-1)/(1+z^-1) | |||
-w_cla | |||
1 + ------ | |||
2 fs | |||
1 - ------------ z^-1 | |||
-w_cla -w_cla | |||
1 - ------ 1 - ------ | |||
2 fs 2 fs | |||
H(z) = ------------ * ----------------------- | |||
-w_cha -w_cha | |||
1 - ------ 1 + ------ | |||
2 fs 2 fs | |||
1 - ------------ z^-1 | |||
-w_cha | |||
1 - ------ | |||
2 fs | |||
We use this design technique, because it is an easy way to obtain a filter | |||
design with the 6 dB/octave rise required of the premphasis filter. | |||
Jackson, Leland B., _Digital_Filters_and_Signal_Processing_Second_Edition_, | |||
Kluwer Academic Publishers, 1989, pp 201-212 | |||
Orfanidis, Sophocles J., _Introduction_to_Signal_Processing_, Prentice Hall, | |||
1996, pp 573-583 | |||
== Parameters == | == Parameters == | ||
; | ; Sample Rate | ||
: | : Sampling frequency in Hz | ||
; | ; Tau | ||
: | : Time constant in seconds (75us in US, 50us in EUR) | ||
; High Corner Freq | |||
: High frequency at which to flatten out (< 0 means default of 0.925*fs/2.0) | |||
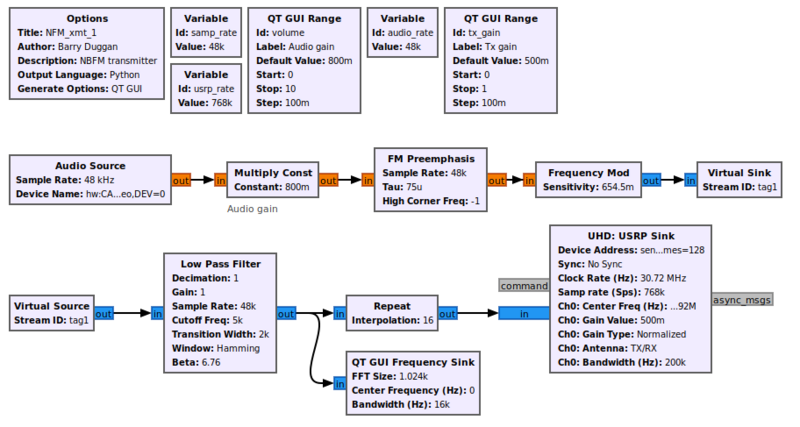
== Example Flowgraph == | == Example Flowgraph == | ||
[[File:NFM_xmt_2_fg.png|800px]] | |||
== Source Files == | == Source Files == | ||
; | ; Python files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/master/gr-analog/python/analog/fm_emph.py] | ||
; Block definition | ; Block definition | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/master/gr-analog/grc/analog_fm_preemph.block.yml] | ||
Latest revision as of 16:04, 27 October 2021
An analog preemphasis filter, that flattens out again at the high end:
C
+-----||------+
| |
o------+ +-----+--------o
| R1 | |
+----/\/\/\/--+ \
/
\ R2
/
\
|
o--------------------------+--------o
(This fine ASCII rendition is based on Figure 5-15 in "Digital and Analog Communication Systems", Leon W. Couch II)
Has this transfer function:
1
s + ---
R1C
H(s) = ------------------
1 R1
s + --- (1 + --)
R1C R2
It has a corner due to the numerator, where the rise starts, at
|Hn(j w_cl)|^2 = 2*|Hn(0)|^2 => s = j w_cl = j (1/(R1C))
It has a corner due to the denominator, where it levels off again, at
|Hn(j w_ch)|^2 = 1/2*|Hd(0)|^2 => s = j w_ch = j (1/(R1C) * (1 + R1/R2))
Historically, the corner frequency of analog audio preemphasis filters been specified by the R1C time constant used, called tau.
So w_cl = 1/tau = 1/R1C; f_cl = 1/(2*pi*tau) = 1/(2*pi*R1*C) w_ch = 1/tau2 = (1+R1/R2)/R1C; f_ch = 1/(2*pi*tau2) = (1+R1/R2)/(2*pi*R1*C)
and note f_ch = f_cl * (1 + R1/R2).
For broadcast FM audio, tau is 75us in the United States and 50us in Europe. f_ch should be higher than our digital audio bandwidth.
The Bode plot looks like this:
/----------------
/
/ <-- slope = 20dB/decade
/
-------------/
f_cl f_ch
In specifying tau for this digital preemphasis filter, tau specifies the *digital* corner frequency, w_cl, desired.
The digital preemphasis filter design below, uses the"bilinear transformation" method of designing digital filters:
1. Convert digital specifications into the analog domain, by prewarping digital frequency specifications into analog frequencies.
w_a = (2/T)tan(wT/2)
2. Use an analog filter design technique to design the filter.
3. Use the bilinear transformation to convert the analog filter design to a digital filter design.
H(z) = H(s)|
s = (2/T)(1-z^-1)/(1+z^-1)
-w_cla
1 + ------
2 fs
1 - ------------ z^-1
-w_cla -w_cla
1 - ------ 1 - ------
2 fs 2 fs
H(z) = ------------ * -----------------------
-w_cha -w_cha
1 - ------ 1 + ------
2 fs 2 fs
1 - ------------ z^-1
-w_cha
1 - ------
2 fs
We use this design technique, because it is an easy way to obtain a filter design with the 6 dB/octave rise required of the premphasis filter.
Jackson, Leland B., _Digital_Filters_and_Signal_Processing_Second_Edition_, Kluwer Academic Publishers, 1989, pp 201-212
Orfanidis, Sophocles J., _Introduction_to_Signal_Processing_, Prentice Hall, 1996, pp 573-583
Parameters
- Sample Rate
- Sampling frequency in Hz
- Tau
- Time constant in seconds (75us in US, 50us in EUR)
- High Corner Freq
- High frequency at which to flatten out (< 0 means default of 0.925*fs/2.0)
Example Flowgraph
Source Files
- Python files
- [1]
- Block definition
- [2]