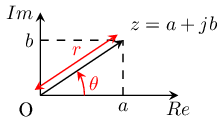User:CSeguinot: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<!-- IQ_complex_signals.mediawiki --> | |||
This | This tutorial originates from discussions on discuss-gnuradio@gnu.org. We will explain why simulating digital communications requires equivalent baseband representation of signal which in fact are complex signals. For this unique reason, complex signals are essential in GNURadio. | ||
This tutorial is intended for non specialist, it involves as less maths as possible and present most results with GNURadio flowgraph. Some examples involving simple modulation scheme used in HAM radio are presented. While introducing complex signal can be seen as increasing complexity, we will see that it drastically simplify some impairment such as synchronization. | |||
If you are searching for more detailed information please refer to corresponding literature such as references [[#ancre1|[1]]],[[#ancre2|[2]]],[[#ancre3|[3]]]. | |||
== Some maths == | |||
This section summarize complex numbers properties used in this tutorial. More information can be found on | |||
[[wikipedia: Complex number|complex number Wikipedia page]]. | |||
[[File:IQ_complex_tutorial_polar2.png|frame|Complex number ''z''=''a'' + ''jb'']] | |||
A complex number is a number of the form ''a'' + ''jb'', where ''a'' and ''b'' are real numbers, and ''j'' is an indeterminate satisfying ''j''<sup>2</sup>=-1 (Mathematician prefer using ''i'' instead of ''j'' used by physicist and radio engineers). For example, z<sub>1</sub>=2+3''j'' is a complex number. The real part Re{''z''} of z<sub>1</sub> is 2 and its imaginary part Im{''z''} is 3. | |||
: <math>z=a+jb \\ \text{Re}\{z\}=a \\ \text{Im}\{z\}=b</math> | |||
==References== | |||
Further reading for complex equivalent baseband signal: | |||
* <span id="ancre1"[1]> [1] Proakis J., ''Digital Communication'', McGraw Hill Series in Electrical and Computer Engineering, Singapore, 1989</span> | |||
* <span id="ancre2"[2]> [2] Gallager R., ''Principles of digital communication'', Cambridge University Press Cambridge, UK, 2008</span> | |||
* <span id="ancre3"[3]> [3] Benedetto S. and Biglieri E., ''Principles of digital transmission : with wireless applications'', Kluwer Academic/Plenum Publishers, NY, 1999</span> | |||
Revision as of 14:08, 21 January 2021
This tutorial originates from discussions on discuss-gnuradio@gnu.org. We will explain why simulating digital communications requires equivalent baseband representation of signal which in fact are complex signals. For this unique reason, complex signals are essential in GNURadio.
This tutorial is intended for non specialist, it involves as less maths as possible and present most results with GNURadio flowgraph. Some examples involving simple modulation scheme used in HAM radio are presented. While introducing complex signal can be seen as increasing complexity, we will see that it drastically simplify some impairment such as synchronization.
If you are searching for more detailed information please refer to corresponding literature such as references [1],[2],[3].
Some maths
This section summarize complex numbers properties used in this tutorial. More information can be found on complex number Wikipedia page.
A complex number is a number of the form a + jb, where a and b are real numbers, and j is an indeterminate satisfying j2=-1 (Mathematician prefer using i instead of j used by physicist and radio engineers). For example, z1=2+3j is a complex number. The real part Re{z} of z1 is 2 and its imaginary part Im{z} is 3.
- Failed to parse (syntax error): {\displaystyle z=a+jb \\ \text{Re}\{z\}=a \\ \text{Im}\{z\}=b}
References
Further reading for complex equivalent baseband signal:
- [1] Proakis J., Digital Communication, McGraw Hill Series in Electrical and Computer Engineering, Singapore, 1989
- [2] Gallager R., Principles of digital communication, Cambridge University Press Cambridge, UK, 2008
- [3] Benedetto S. and Biglieri E., Principles of digital transmission : with wireless applications, Kluwer Academic/Plenum Publishers, NY, 1999