FM Deemphasis
An analog deemphasis filter:
R
o------/\/\/\/---+----o
|
= C
|
---
Has this transfer function:
1 1
---- ---
RC tau
H(s) = ---------- = ----------
1 1
s + ---- s + ---
RC tau
And has its -3 dB response, due to the pole, at
|H(j w_c)|^2 = 1/2 => s = j w_c = j (1/(RC))
Historically, this corner frequency of analog audio deemphasis filters been specified by the RC time constant used, called tau. So w_c = 1/tau.
FWIW, for standard tau values, some standard analog components would be:
tau = 75 us = (50K)(1.5 nF) = (50 ohms)(1.5 uF) tau = 50 us = (50K)(1.0 nF) = (50 ohms)(1.0 uF)
In specifying tau for this digital deemphasis filter, tau specifies the *digital* corner frequency, w_c, desired.
The digital deemphasis filter design below, uses the "bilinear transformation" method of designing digital filters:
1. Convert digital specifications into the analog domain, by prewarping digital frequency specifications into analog frequencies.
w_a = (2/T)tan(wT/2)
2. Use an analog filter design technique to design the filter.
3. Use the bilinear transformation to convert the analog filter design to a digital filter design.
H(z) = H(s)|
s = (2/T)(1-z^-1)/(1+z^-1)
w_ca 1 1 - (-1) z^-1
H(z) = ---- * ----------- * -----------------------
2 fs -w_ca -w_ca
1 - ----- 1 + -----
2 fs 2 fs
1 - ----------- z^-1
-w_ca
1 - -----
2 fs
We use this design technique, because it is an easy way to obtain a filter design with the -6 dB/octave roll-off required of the deemphasis filter.
Jackson, Leland B., _Digital_Filters_and_Signal_Processing_Second_Edition_, Kluwer Academic Publishers, 1989, pp 201-212
Orfanidis, Sophocles J., _Introduction_to_Signal_Processing_, Prentice Hall, 1996, pp 573-583
Parameters
- Sample Rate
- Sampling frequency in Hz
- Tau
- Time constant in seconds (75us in US, 50us in EUR)
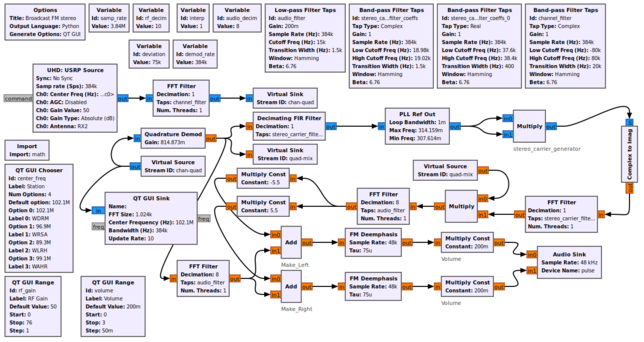
Example Flowgraph
This flowgraph implements a Broadcast FM stereo receiver using basic blocks.
Source Files
- Python files
- [1]
- Block definition
- [2]