Scrambler

The Scrambler block is an implementation of a multiplicative scrambler. It takes an input bit stream and randomizes it using a linear feedback shift register (LFSR) where the feedback is fed into the LFSR itself.

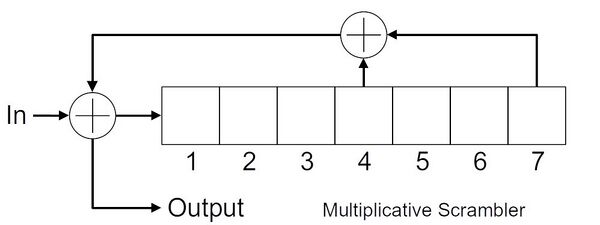
This is a block diagram of a 7-stage multiplicative scrambler with a LFSR with feedback taps (7,4).

This block works on the LSB only of the input data stream, i.e., on an "unpacked binary" stream, and produces the same format on its output.

Parameters

Mask

Polynomial mask for LFSR. To calculate the required mask, reverse the order of the desired polynomial. For example, a maximal-length 7-stage LFSR could use taps (7,4). A mask for this implementation would be the binary value 0b001001, or in hex 0x5. A 5-stage LFSR with taps (5,3) would be 0b00101, or in hex 0x5. Even though both have the same mask, the Scrambler block would implement them different due to the Length values for each (6 for the 7-stage, and 4 for the 5-stage).

Seed

Initial shift register contents. This is the fill condition of the LFSR.

Length

Shift register length. This is one less than the polynomial size. For example, if a 7-stage LFSR also means a polynomial size of 7. The Length of this, for this block, would be 6.

Example Flowgraph

Insert description of flowgraph here, then show a screenshot of the flowgraph and the output if there is an interesting GUI. Currently we have no standard method of uploading the actual flowgraph to the wiki or git repo, unfortunately. The plan is to have an example flowgraph showing how the block might be used, for every block, and the flowgraphs will live in the git repo.

Here is a simple python-function to create the mask and length from the exponents of a polynomial:

 def make_mask(*exp):
     from functools import reduce
     return reduce(int.__xor__,map(lambda x:2**x,exp)),max(exp)-1
 mask,k = make_mask(5,3,0) # mask and length for p(x) = x^5 + x^3 + 1, a primitive polynomial in GF(2)

Source Files

C++ files

TODO

Header files

TODO

Public header files

TODO

Block definition

TODO