FFT
This block takes in a vector of floats or complex values and calculates the FFT. If all you do is want to see the frequency domain of a signal, the QT GUI Frequency Sink is more user friendly.
Note that even if the input signal is real, the output will be complex, so you must use a Complex to Mag or similar block if you want to see magnitude.
Parameters
- FFT Size
- Number of samples used in each FFT calculation, which also determines how many points are in the output.
- Forward/Reverse
- Whether to do an FFT or IFFT.
- Window
- Type of window to apply to each set of samples before the FFT is taken, default is a blackmanharris window. The argument of the window.blackmanharris() function is simply how many points in the window, which must match the FFT size. If an empty window "[]" is supplied then no windowing math is performed.
- Shift
- Whether or not to do an "fft shift" which puts DC (0 Hz) in the center. If you are not sure what this means, leave it set to Yes. Only active when input type is complex.
- Num Threads
- Number of threads to assign to perform the FFTs.
Example Flowgraph
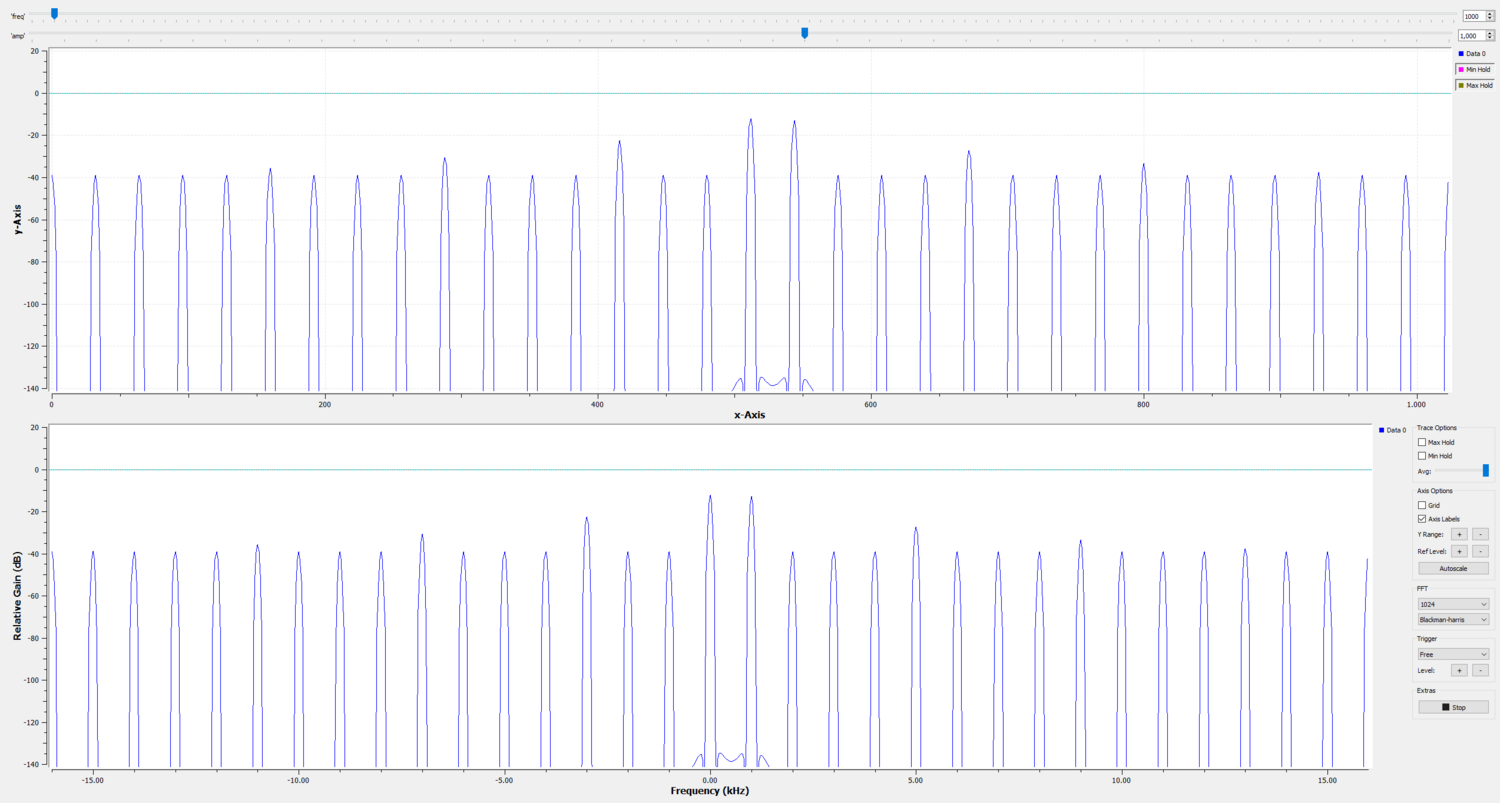
This flowgraph shows how the FFT block can be used to reproduce the behavior of the QT GUI Frequency Sink block. Both outputs match, but using the FFT block directly requires converting from a stream to vector, and performing the magnitude and log manually.
The 'fast multiply const' block multiplies by 1/vector_length. The Log10 block multiplies also by 10 (n=10).
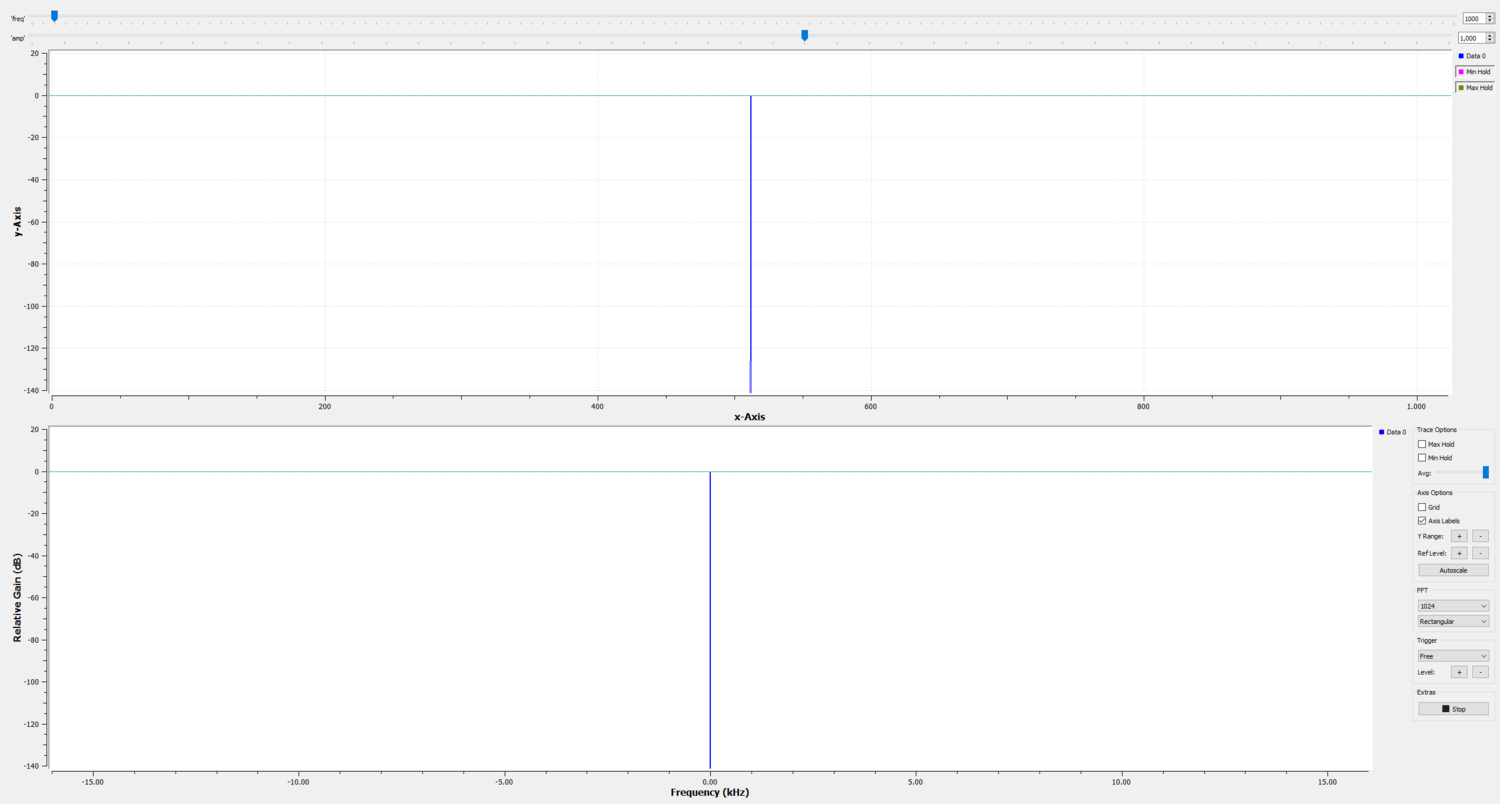
Injecting a constant value waveform (amplitude of 1) and applying a rectangular window gives us an impulse (Dirac delta). The peak value has its maximum value at 0 dBfs, telling us that the reference is a vector containing ones.
Source Files
- C++ files
- Complex input
- Real input
- Core algorithms
- Header files
- Complex input
- Real input
- Public header files
- Complex input
- Real input
- Block definition
- GRC yaml