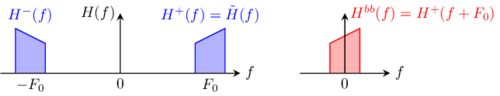IQ Complex Tutorial: Difference between revisions
| (40 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
<!-- | <!-- IQ_complex_Signal_Tutorial --> | ||
This tutorial originates from discussions on discuss-gnuradio@gnu.org. We will explain why simulating digital communications requires equivalent baseband representation of | This tutorial originates from discussions on discuss-gnuradio@gnu.org. We will explain why simulating digital communications requires equivalent baseband representation of signals--which in fact are complex signals. For this reason, complex signals are essential in GNURadio. | ||
This tutorial is also intended for non | This tutorial is also intended for non-specialists, as it involves as little maths as possible while presenting most results using GNURadio's flowgraph. Some examples involving simple modulation schemes used in HAM radio are presented. While introducing complex signals can be seen as increasing complexity, we will see that it drastically simplifies the understanding of certain concepts, such as synchronization. | ||
If you are searching for more detailed information please refer to | If you are searching for more detailed information, please refer to the literature--such as references [[#ancre1|[1]]],[[#ancre2|[2]]],[[#ancre3|[3]]]. | ||
== Some maths == | == Some maths == | ||
This section | This section summarizes complex number properties used in this tutorial. More information can be found on | ||
[[wikipedia: Complex number|complex number Wikipedia page]]. | [[wikipedia: Complex number|complex number Wikipedia page]]. | ||
[[File:IQ_complex_tutorial_polar2.png|frame|Complex number ''z''=''a'' + ''jb'']] | [[File:IQ_complex_tutorial_polar2.png|frame|Complex number ''z''=''a'' + ''jb'']] | ||
A complex number is a number of the form ''a'' + ''jb'', where ''a'' and ''b'' are real numbers, and ''j'' is an indeterminate satisfying ''j''<sup>2</sup>=-1 (Mathematician prefer using ''i'' instead of ''j'' used by physicist and radio engineers). For example, z<sub>1</sub>=2+ | A complex number is a number of the form ''a'' + ''jb'', where ''a'' and ''b'' are real numbers, and ''j'' is an indeterminate satisfying ''j''<sup>2</sup>=-1 (Mathematician prefer using ''i'' instead of ''j'' used by physicist and radio engineers). For example, z<sub>1</sub>=2 + ''j''3 is a complex number. The real part Re{''z''} of z<sub>1</sub> is 2 and its imaginary part Im{''z''} is 3. | ||
<math>z=a+jb </math> | |||
<math>\text{Re}\{z\}=a</math> | |||
<math>\text{Im}\{z\}=b</math> | |||
| Line 23: | Line 23: | ||
: <math>r=|z|=\sqrt{a^2+b^2}</math> | : <math>r=|z|=\sqrt{a^2+b^2}</math> | ||
The phase φ of ''z'' | The phase φ of ''z'' (referred to as the ''argument'') is the angle of the radial Oz on the positive real axis. | ||
: <math>\phi=\arg(z)=\arctan(b/a) </math> (for a≠0) | : <math>\phi=\arg(z)=\arctan(b/a) </math> (for a≠0) | ||
Together, r and φ | Together, r and φ provide another means of representing complex numbers--both the polar and exponential forms. | ||
: <math>z=r \left(cos(\phi) + j sin(\phi) \right) = r e^{j\phi}</math> | : <math>z=r \left(cos(\phi) + j sin(\phi) \right) = r e^{j\phi}</math> | ||
| Line 35: | Line 35: | ||
: <math>z_1= r_1 e^{j\phi_1}</math> | : <math>z_1= r_1 e^{j\phi_1}</math> | ||
: <math> | : <math>z_2= r_2 e^{j\phi_2}</math> | ||
: <math>z=z_1z_2= r_1r_2 e^{j(\phi_1+\phi_2)}</math> | : <math>z=z_1z_2= r_1r_2 e^{j(\phi_1+\phi_2)}</math> | ||
The following complex numbers have a unit magnitude ''r''=1 : | |||
: <math>+1=e^{j0}</math> | : <math>+1=e^{j0}</math> | ||
| Line 45: | Line 45: | ||
: <math>-j=e^{j3\pi/2} </math> | : <math>-j=e^{j3\pi/2} </math> | ||
A complex signal ''c(t)'' can be seen as two real | A complex signal ''c(t)'' can be seen as two real signals ''a(t), b(t)''--often written as ''i(t), q(t)''--and combined to create a complex signal. It can also be represented by its amplitude over time ''r(t)'' as well as its phase variation over time ''φ(t)'' | ||
: <math>c(t) = | : <math>c(t) = a(t) + j b(t) = r(t) e^{j\phi (t)} </math> | ||
== Why we need complex and IQ signals == | == Why we need complex and IQ signals == | ||
GNURadio software is mainly used to design and study radio communications. Making high frequency transmission requires modulating a high frequency carrier | GNURadio software is mainly used to design and study radio communications. Making high frequency transmission requires modulating a high frequency carrier of frequency ''f<sub>0</sub>''. The most common modulation for analog transmissions are: amplitude modulation (AM), phase modulation (PM), and frequency modulation (FM). | ||
[[File:IQ_complex_tutorial_AM_spectrum.png|thumb|400px|AM spectrum]] | [[File:IQ_complex_tutorial_AM_spectrum.png|thumb|400px|AM spectrum]] | ||
For analog AM, the modulated signal ''m(t)'' is simply the mathematical product of the carrier ''c(t)'' and the baseband signal | For analog AM, the modulated signal ''m(t)'' is simply the mathematical product of the carrier ''c(t)'' and the baseband signal ''a(t)''. The corresponding hardware is a mixer whose scheme and mathematical representation is a multiplier. | ||
: <math>m(t) = a(t) c(t) = a(t) \cos(2\pi f_0t)</math> | : <math>m(t) = a(t) c(t) = a(t) \cos(2\pi f_0t)</math> | ||
We call ''a(t)'' a baseband signal since its spectrum is in a low frequency range starting near 0 Hz ( | We call ''a(t)'' a baseband signal since its spectrum is in a low frequency range--starting near 0 Hz (e.g. [0-20kHz] for a HiFi audio signal). | ||
The spectrum of an AM modulated signal ''M(f)'' is the translation | The spectrum of an AM modulated signal ''M(f)'' is the translation of the audio spectrum ''A(f)'' around ±''F<sub>0</sub>'' with ''A(f)'' being the entire spectrum of the modulating signal, using both positive and negative frequencies | ||
: <math>M(f) = \frac{1}{2}\big(A(f-f_0) + A(f+f_0)\big)</math> | : <math>M(f) = \frac{1}{2}\big(A(f-f_0) + A(f+f_0)\big)</math> | ||
Important - Negative frequencies are often omitted in spectrum representation since, for real signal (''a(t)'', ''m(t)'' are real) the power spectrum are symmetric around zero (more details on this later). | |||
Up to now we have been dealing with real | Up to now we have been dealing with real signals. The need for complex signals appears in the next step. Simulation requires sampled signal. Sampling is the operation of observing a continuous signal and taking a finite number of samples at a given sampling rate ''f<sub>s</sub>'' (i.e. one sample each 1/''f<sub>s</sub>'' second). Because a simulator can only make calculations on a finite number of samples, it requires a sampled signal. Nyquist Sampling theorem states that the sampling rate must be greater than twice the maximum frequency ''F<sub>Max</sub>'' in order to reconstruct the original signal from the sampled signal. | ||
: <math>f_s > | : <math>f_s > 2F_{Max}</math> | ||
For | For a HiFi audio signal, the maximum audio frequency <math>F_{Max Audio}</math> is close to 20 kHz, so the sampling rate must be higher than 40 kHz (44.1 kHz is often used in computer sound cards, 8 kHz is used for mobile phones since voice has a lower frequency range than HiFi audio). | ||
For an AM signal modulated by an audio signal, maximum frequency of the modulated spectrum is <math>F_{Max}=F_0+F_{Max Audio}</math>. Direct sampling of such signal is not possible with conventional hardware such as low cost SDR dongle. If the carrier frequency is close to 1 GHz, the sampling rate should be at least 2 GHz. This is obviously too much | For an AM signal modulated by an audio signal, the maximum frequency of the modulated spectrum is <math>F_{Max}=F_0+F_{Max Audio}</math>. Direct sampling of such a signal is not possible with conventional hardware such as a low cost SDR dongle. If the carrier frequency is close to 1 GHz, the sampling rate should be at least 2 GHz. This is obviously too much for the computer to handle (higher than some CPU clocks). | ||
Flowgraph [[Media:IQ_tutorial_AM_TX_real.grc|IQ_tutorial_AM_TX_real.grc]] illustrates amplitude modulation using only real blocks (excepted for bits source). As a consequence, the maximum carrier frequency is limited to several tens of kHz. | Flowgraph [[Media:IQ_tutorial_AM_TX_real.grc|IQ_tutorial_AM_TX_real.grc]] illustrates amplitude modulation using only real blocks (excepted for bits source). As a consequence, the maximum carrier frequency is limited to several tens of kHz. | ||
* study the modulator part which simply | * study the modulator part which simply multiplies the baseband signal and the sinusoidal carrier | ||
* look at the influence of the carrier frequency on the modulated signal spectrum (carrier frequency must stay lower than half the sampling rate) | * look at the influence of the carrier frequency on the modulated signal spectrum (carrier frequency must stay lower than half the sampling rate) | ||
* look at the spectrum shape for sawtooth input and random bit sequence (QT | * look at the spectrum shape for sawtooth input and random bit sequence (QT GUI chooser and selector) | ||
* When transmitting random bits, you can | * When transmitting random bits, you can deactivate the interpolating FIR Filter and replace it by a root raised cosine filter | ||
== | == Spectral properties of signals == | ||
Amplitude spectrum is calculated using the Fourier Transform. It represents how the power is spread in the frequency domain. It allows for determining the signal bandwidth. Power Spectral Density or PSD correspond to the average magnitude of the Amplitude spectrum. | Amplitude spectrum is calculated using the Fourier Transform. It represents how the power is spread in the frequency domain. It allows for determining the signal bandwidth. Power Spectral Density or PSD correspond to the average magnitude of the Amplitude spectrum. | ||
In this section we summarize some properties of the phase arg''{X(f)}'' and magnitude |''X(f | In this section we summarize some properties of the phase arg''{X(f)}'' and magnitude |''X(f)''|. We first consider properties for continuous signal. Then we will investigate additional properties of sampled signal (those used in GNURadio). | ||
Given a signal ''x(t) | Given a signal ''x(t)'' its amplitude/phase spectrum is denoted ''X(f)'' which is a complex function given by : | ||
: <math>X(f) =\int{x(t)e^{-2j\pi ft}}dt</math> | : <math>X(f) =\int{x(t)e^{-2j\pi ft}}dt</math> | ||
=== continuous real signal === | === continuous real signal === | ||
Every real signal | Every real signal has a spectrum whose magnitude is symmetric and phase is anti-symmetric. | ||
: <math>x(t) \in \mathbb{R}</math> | : <math>x(t) \in \mathbb{R}</math> | ||
: <math>X(-f)=X^*(f)</math> | : <math>X(-f)=X^*(f)</math> | ||
| Line 95: | Line 95: | ||
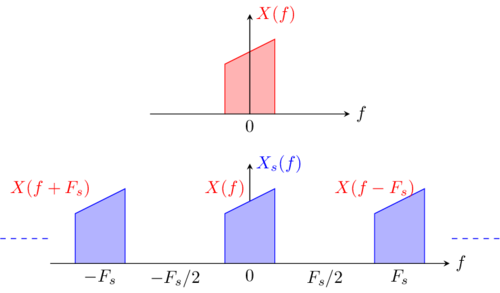
[[File:IQ_complex_tutorial_complex_spectrum.png|thumb|500px|Complex signal spectrum and, sampled complex signal spectrum (only first 3 patterns represented)]] | [[File:IQ_complex_tutorial_complex_spectrum.png|thumb|500px|Complex signal spectrum and, sampled complex signal spectrum (only first 3 patterns represented)]] | ||
=== continuous complex signal === | === continuous complex signal === | ||
The main difference with real signal is that: | The main difference with real signal is that: | ||
* any complex signal having non null imaginary part exhibits a non-symmetric spectrum. | * any complex signal having non null imaginary part exhibits a non-symmetric spectrum. | ||
* as a consequence, every non-symmetric spectrum | * as a consequence, every non-symmetric spectrum corresponds to a complex signal | ||
=== sampled signals === | === sampled signals === | ||
We consider a signal ''x(t | We consider a signal ''x(t)'' and we note its sampled version ''x<sub>s</sub>(t)'' sampled at frequency ''F<sub>s</sub>''. | ||
The spectrum ''X<sub>s</sub>(f)'' of the sampled signal is a periodic function of period ''F<sub>s</sub>''. | The spectrum ''X<sub>s</sub>(f)'' of the sampled signal is a periodic function of period ''F<sub>s</sub>''. | ||
: <math>X_s(f)= | : <math>X_s(f)= X(f-kF_s)</math> | ||
So the sampled signal spectrum verify : | So the sampled signal spectrum verify : | ||
: <math>X_s(f+kF_s)=X_s(f)</math> | : <math>X_s(f+kF_s)=X_s(f)</math> | ||
Generally the bandwidth of ''X(f | Generally the bandwidth of ''X(f)'' is lower then ''F<sub>s</sub>''/2. The infinite sum defined above exhibit no aliasing (no superposition of patterns ''X(f)'', ''X(f+F<sub>s</sub>)'' and ''X(f-F<sub>s</sub>)''). In that case, as stated in the Nyquist theorem of sampling, the original spectrum/signal can be recovered by filtering the sampled signal. | ||
When the maximum frequency of the signal spectrum do not respect Nyquist theorem, one should filter the signal with a low pass filter having a cutt-off frequency lower then ''F<sub>s</sub>''/2 before sampling: this correspond to the anti-aliasing filter used in every SDR hardware. | When the maximum frequency of the signal spectrum do not respect Nyquist theorem, one should filter the signal with a low pass filter having a cutt-off frequency lower then ''F<sub>s</sub>''/2 before sampling: this correspond to the anti-aliasing filter used in every SDR hardware. | ||
== Complex | == Complex envelope, equivalent baseband signal== | ||
Baseband signals have a spectrum at low frequency near 0 Hz. Audio, video and NRZ line code are baseband signals. | Baseband signals have a spectrum at low frequency near 0 Hz. Audio, video and NRZ line code are baseband signals. | ||
Passband signals have no energy near 0 Hz and a spectrum located near a high frequency (generally the carrier frequency). Analog and digital AM, PM and FM modulated signals are passband signals. | |||
A theorem ([[#ancre1|[1]]],[[#ancre2|[2]]],[[#ancre3|[3]]]) states that any high frequency | A theorem ([[#ancre1|[1]]],[[#ancre2|[2]]],[[#ancre3|[3]]]) states that any high frequency passband signal having a limited bandwidth ''B'' can be represented by a baseband equivalent signal having the same bandwidth. This baseband equivalent signal also called the complex envelope is used in simulators since it allows to lower sampling rate as compared to directly sampling the passband signal. | ||
The equivalent baseband representation | The equivalent baseband representation helps us for the simulation of passband signals. At this step we need some math. We will consider a carrier modulated in phase and/or amplitude (in the sake of simplicity, Frequency modulation is not considered but it can be related to phase modulation.). Such a modulated signal ''m(t)'' and it's complex representation <math>\tilde{m}(t)</math> is : | ||
: <math>m(t)=a(t) \cos(2\pi F_0t + \phi(t))</math> | : <math>m(t)=a(t) \cos(2\pi F_0t + \phi(t))</math> | ||
: <math>\tilde{m}(t)=a(t) e^{ | : <math>\tilde{m}(t)=a(t) e^{j(2\pi F_0t + \phi(t))} = a(t) e^{j \phi(t)} e^{j2\pi F_0t} = m^{bb}(t) e^{j2\pi F_0t}</math> | ||
For modulated signal, the complex representation is obtained by replacing the cos function by an exponent function . For a more general definition see [[#ancre1|[1]]],[[#ancre2|[2]]],[[#ancre3|[3]]] . The real signal | For modulated signal, the complex representation is obtained by replacing the cos function by an exponent function . For a more general definition see [[#ancre1|[1]]],[[#ancre2|[2]]],[[#ancre3|[3]]] . The real signal corresponds to the real part of the complex signal <math>m(t)=\text{Re}(\tilde{m}(t))</math>. | ||
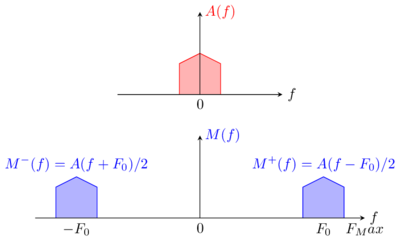
[[File:IQ_complex_tutorial_EQ_BB.png|thumb|400px|AM spectrum]] | [[File:IQ_complex_tutorial_EQ_BB.png|thumb|400px|AM spectrum]] | ||
| Line 133: | Line 134: | ||
where <math>=M^+(f)</math> denotes the restriction of <math>=M(f)</math> to the positive frequency range. | where <math>=M^+(f)</math> denotes the restriction of <math>=M(f)</math> to the positive frequency range. | ||
Let us now look at the complex envelope or equivalent baseband signal <math>m^{bb}(t)</math> of | Let us now look at the complex envelope or equivalent baseband signal <math>m^{bb}(t)</math> of passband signal <math>m(t)</math> defined by : | ||
: <math>m^{bb}(t)= \tilde{m}(t) e^{ | : <math>m^{bb}(t)= \tilde{m}(t) e^{-j2\pi F_0t} = a(t) e^{j \phi(t)} </math> | ||
Multiplying a signal by <math>e^{+j2\pi F_0t}</math> correspond to a frequency translation of the spectrum so that we have: | Multiplying a signal by <math>e^{+j2\pi F_0t}</math> correspond to a frequency translation of the spectrum so that we have: | ||
:<math>M^{bb}(f)=M+(f+F_0)</math> | :<math>M^{bb}(f)=M^+(f+F_0)</math> | ||
So the spectrum of the complex | So the spectrum of the complex envelope is a baseband signal whose spectrum has the same shape as <math>=M^+(f)</math>. For this reason, knowing <math>\tilde{m}(t)</math> or <math>M^{bb}(f)</math> is sufficient to reconstruct <math>m(t)</math> or <math>M(f)</math>. | ||
=== Equivalent baseband, | === Equivalent baseband, Envelope, Complex signals? === | ||
Terms '''equivalent baseband signal''', '''complex envelope''' and '''complex signal''' can be seen as equivalent terms referring to the same thing. | Terms '''equivalent baseband signal''', '''complex envelope''' and '''complex signal''' can be seen as equivalent terms referring to the same thing. | ||
While simulating some radio we have mainly two type of signals: | While simulating some radio we have mainly two type of signals: | ||
* any low frequency or baseband signal are real signal, they are represented by real signals | * any low frequency or baseband signal are real signal, they are represented by real signals | ||
* every | * every passband signal must be represented by their equivalent baseband complex signal (excepted for systems having very low carrier frequency) | ||
So in a gnuradio flowgraph, there is no ambiguity: every complex signal ( | So in a gnuradio flowgraph, there is no ambiguity: every complex signal (blue interconnections) is implicitly an equivalent representation of a passband signal so we will simply call it a '''complex signal'''. | ||
== IQ modulator and demodulator== | == IQ modulator and demodulator== | ||
[[File:IQ_complex_tutorial_IQ.png|thumb|200px|Complex signal in the IQ plane]] | [[File:IQ_complex_tutorial_IQ.png|thumb|200px|Complex signal in the IQ plane]] | ||
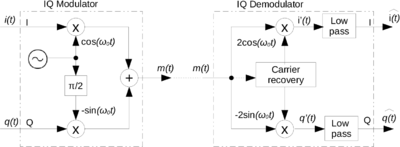
[[File:IQ_complex_tutorial_IQ_Mod_Demod-crop.png|thumb|400px| | [[File:IQ_complex_tutorial_IQ_Mod_Demod-crop.png|thumb|400px|IQ modulator and demodulator]] | ||
Let us now come to hardware and SDR and first rewrite the equivalent baseband signal and the modulated signal ''m(t)'' : | Let us now come to hardware and SDR and first rewrite the equivalent baseband signal and the modulated signal ''m(t)'' : | ||
: <math>m^{bb}(t)=a(t) e^{j \phi(t)} =i(t) + j q(t)</math> | : <math>m^{bb}(t)=a(t) e^{j \phi(t)} =i(t) + j q(t)</math> | ||
: <math>m(t)=\text{Re} \left[ \big(i(t)+jq(t)\big) e^{j2\pi F_0t} \right]</math> | : <math>m(t)=\text{Re} \left[ \big(i(t)+jq(t)\big) e^{j2\pi F_0t} \right]</math> | ||
: <math>m(t)=i(t) \cos(2\pi F_0t) -q(t | : <math>m(t)=i(t) \cos(2\pi F_0t) -q(t) \sin(2\pi F_0t)</math> | ||
The phase ''φ(t)'' of the modulated signal ''m(t)'', is identical to the phase of the complex signal ''c(t)=i(t)+jq(t)''. The equivalent baseband signal ''c(t)'' is represented in a complex plane also refeered to as the IQ plane. The resulting ''m(t)'' can be any modulated in AM, PM or even FM signal. | The phase ''φ(t)'' of the modulated signal ''m(t)'', is identical to the phase of the complex signal ''c(t)=i(t)+jq(t)''. The equivalent baseband signal ''c(t)'' is represented in a complex plane also refeered to as the IQ plane. The resulting ''m(t)'' can be any modulated in AM, PM or even FM signal. | ||
| Line 165: | Line 166: | ||
As a result, the modulated signal ''m(t)'' is the addition of : | As a result, the modulated signal ''m(t)'' is the addition of : | ||
* <math>i(t) \cos(2\pi F_0t)</math> which is an AM modulated signal, the product of ''i(t)'' by a signal In phase with the carrier (i stand for In phase) | * <math>i(t) \cos(2\pi F_0t)</math> which is an AM modulated signal, the product of ''i(t)'' by a signal In phase with the carrier (i stand for In phase) | ||
* <math>q(t) \sin( | * <math>-q(t) \sin(2\pi F_0t)</math> which is an AM modulated signal, the product of ''q(t)'' by a signal in Quadrature with the carrier (q stand for Quadrature) | ||
The corresponding hardware is called an IQ modulator. Every modern radio communication uses IQ modulator for emitting and IQ demodulator for receiving. The IQ demodulator is able to recover incoming ''i(t)'' and ''q(t)''. If the amplitude of the recovered carrier is 2, and if modulator and demodulator carrier are synchronous (same frequency and phase) the output of the IQ demodulator correspond to input ''i(t)'' and ''q(t)''. | The corresponding hardware is called an IQ modulator. Every modern radio communication uses IQ modulator for emitting and IQ demodulator for receiving. The IQ demodulator is able to recover incoming ''i(t)'' and ''q(t)''. If the amplitude of the recovered carrier is 2, and if modulator and demodulator carrier are synchronous (same frequency and phase) the output of the IQ demodulator correspond to input ''i(t)'' and ''q(t)''. | ||
| Line 173: | Line 174: | ||
In real hardware, carrier are not synchronous and the receiver must compensate any phase and frequency difference between emitter and receiver. This is done using some hardware and/or software such as polyphase clock sync, and Costas loop. | In real hardware, carrier are not synchronous and the receiver must compensate any phase and frequency difference between emitter and receiver. This is done using some hardware and/or software such as polyphase clock sync, and Costas loop. | ||
SDR Module such as USRP [https://www.ettus.com/all-products/usrp-n320/|(USRP N320 block Diagram)] and SDR Dongle [https://www.programmersought.com/article/59454592969/| (RTL-2832)] input and output are the 2 real signals ''i(t)'' and ''q(t)'' combined to form the complex signal ''i(t) + j q(t)'' which turns to be the equivalent baseband of the modulated emitted or received signal. These hardware are based on IQ modulator and IQ demodulator associated with mixers when intermediate frequency (IF) is used. | SDR Module such as USRP [https://www.ettus.com/all-products/usrp-n320/| (USRP N320 block Diagram)] and SDR Dongle [https://www.programmersought.com/article/59454592969/| (RTL-2832)] input and output are the 2 real signals ''i(t)'' and ''q(t)'' combined to form the complex signal ''i(t) + j q(t)'' which turns to be the equivalent baseband of the modulated emitted or received signal. These hardware are based on IQ modulator and IQ demodulator associated with mixers when intermediate frequency (IF) is used. | ||
== Some examples of EqBB signals == | == Some examples of EqBB signals == | ||
| Line 183: | Line 184: | ||
We will consider a pure sine wave, close to the carrier having a ''Δf'' frequency shift and ''φ'' phase shift as compared to the carrier. After some math we get its complex equivalent signal. | We will consider a pure sine wave, close to the carrier having a ''Δf'' frequency shift and ''φ'' phase shift as compared to the carrier. After some math we get its complex equivalent signal. | ||
: <math>m(t) = A \cos (2\pi (F_0+\Delta f)t+ \phi)</math> | : <math>m(t) = A \cos (2\pi (F_0+\Delta f)t+ \phi)</math> | ||
: <math>\tilde{m}(t) = A e^{ | : <math>\tilde{m}(t) = A e^{j(2\pi (F_0+\Delta f)t + \phi)} </math> | ||
: <math>m^{bb}(t) = A e^{ | : <math>m^{bb}(t) = A e^{j(2\pi\Delta f t+ \phi)} = A e^{j 2\pi \Delta ft} e^{j\phi}</math> | ||
The complex envelope of the carrier itself is found for ''Δf''=0 and ''φ''=0 which yields <math>m^{bb}(t) = A</math>. We conclude that in a GNURadio flowgraph, the carrier is represented by a continuous components, a pure DC signal ; this may | The complex envelope of the carrier itself is found for ''Δf''=0 and ''φ''=0 which yields <math>m^{bb}(t) = A</math>. We conclude that in a GNURadio flowgraph, the carrier is represented by a continuous components, a pure DC signal ; this may seem counter intuitive. The spectrum <math>M^{bb}(f)</math> is a single peak at ''f=0'' which can be represented using the Dirac ''δ(f) function (or distribution)'' : <math>M^{bb}(f)=\delta(f))</math>. Shifting this spectrum of <math>+F_0</math> towards positive frequency we get the positive part of the carrier spectrum (a peak at <math>+F_0</math>) : <math>M^+(f)=\delta(f-F_0))</math>. The negative part of the spectrum is simply obtained by symmetry of the real part (a peak at <math>-F_0</math>). | ||
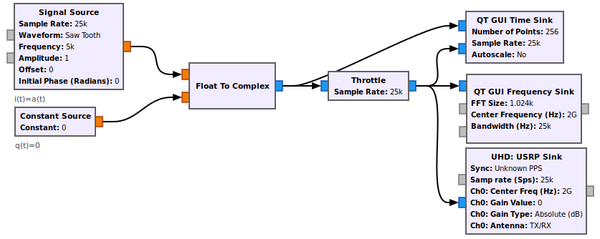
This can be simulated with GNURadio flowgraph [[media:IQ_tutorial_eq_bb.grc|IQ_tutorial_eq_bb.grc]]. The spectrum of our carrier is centered at 0 Hz. The Frequency sink has a feature to shift this spectrum around <math>F_0</math> which is a parameter of the sink. In a simulation, it is not necessary to represent the negative part of the spectrum since ''m(t'') being real, it spectrum is obviously symmetric. | This can be simulated with GNURadio flowgraph [[media:IQ_tutorial_eq_bb.grc|IQ_tutorial_eq_bb.grc]]. The spectrum of our carrier is centered at 0 Hz. The Frequency sink has a feature to shift this spectrum around <math>F_0</math> which is a parameter of the sink. In a simulation, it is not necessary to represent the negative part of the spectrum since ''m(t'') being real, it spectrum is obviously symmetric. | ||
We will now consider ''Δf'' ≠0 which simulate a signal not exactly synchronous to the carrier. This | We will now consider ''Δf'' ≠0 which simulate a signal not exactly synchronous to the carrier. This yields | ||
: <math>m^{bb}(t) = A e^{ | : <math>m^{bb}(t) = A e^{j 2\pi \Delta ft}</math> | ||
The complex | The complex envelope is rotating vector (you can simulate this with ''Δf''=1 Hz giving a vector which rotate at 60 rpm or 1 turn per second) , its spectrum is a single peak at ''f=+Δf''. This complex signal exhibits a non symmetric spectrum (no peak at ''f=-Δf''). Change ''Δf'' to -0.5 Hz, the vector now rotates counter clockwise at 30 rpm or 0.5 turn per second. | ||
Exercise: | |||
Open flowgraph [[media:IQ_tutorial_eq_bb.grc|IQ_tutorial_eq_bb.grc]]. Parameter delta_f is set with an increment of 1/12, which correspond to 5 rotation per minute. | Open flowgraph [[media:IQ_tutorial_eq_bb.grc|IQ_tutorial_eq_bb.grc]]. Parameter delta_f is set with an increment of 1/12, which correspond to 5 rotation per minute. | ||
* For ''Δf''=1/12=0.0833, what is the speed of rotation of the complex signal? | * For ''Δf''=1/12=0.0833, what is the speed of rotation of the complex signal? | ||
| Line 201: | Line 202: | ||
* Do the same for a negative ''Δf'' | * Do the same for a negative ''Δf'' | ||
* For ''Δf =f<sub>s</sub>'' what is the equivelant baseband frequency. What is the carrier frequency ? | * For ''Δf =f<sub>s</sub>'' what is the equivelant baseband frequency. What is the carrier frequency ? | ||
* Set ''Δf''=0 and ''φ''≠0. | * Set ''Δf''=0 and ''φ''≠0. Discuss the simulated equivalent baseband signal. | ||
=== AM mod demod example=== | === AM mod demod example=== | ||
This example will consider signal baseband signal ''a(t)'' modulating a carrier at F<sub>0</sub> in AM, and its demodulation. As no phase modulation in used, ''φ(t)''=0 and consequently ''q(t)''=0. | This example will consider signal baseband signal ''a(t)'' modulating a carrier at F<sub>0</sub> in AM, and its demodulation. As no phase modulation in used, ''φ(t)''=0 and consequently ''q(t)''=0. | ||
: <math>m(t) = a(t) \cos (2\pi | : <math>m(t) = a(t) \cos (2\pi F_0 t)=i(t) \cos (2\pi F_0t) -q(t) \sin (2\pi F_0t) </math> | ||
: <math>i(t) = a(t) </math> | : <math>i(t) = a(t) </math> | ||
: <math>q(t) = 0</math> | : <math>q(t) = 0</math> | ||
| Line 218: | Line 219: | ||
* the upper one uses real signals. It is the exact AM modulator uses at the beginning of this tutorial. | * the upper one uses real signals. It is the exact AM modulator uses at the beginning of this tutorial. | ||
** sampling frequency is 200 kHz, 40 times the input rate which equal 5 kHz. | ** sampling frequency is 200 kHz, 40 times the input rate which equal 5 kHz. | ||
** allowing a maximum carrier frequency close to | ** allowing a maximum carrier frequency close to 100kHz | ||
[[File:IQ complex tutorial AM TX complex.png|thumb|600px|AM modulator flowgraph]] | [[File:IQ complex tutorial AM TX complex.png|thumb|600px|AM modulator flowgraph]] | ||
| Line 257: | Line 258: | ||
Running this flowgraph, demodulation is obtained taking the real part (imperfect solution), or the magnitude (good solution) of the complex signal. | Running this flowgraph, demodulation is obtained taking the real part (imperfect solution), or the magnitude (good solution) of the complex signal. | ||
* these two methods give exactly the same results | * these two methods give exactly the same results | ||
* these two methods are close to, but differ from original input signal due to the low-pass filter (only 6 peak are taken from the sawtooth spectrum, 3 for positive frequency and 3 | * these two methods are close to, but differ from original input signal due to the low-pass filter (only 6 peak are taken from the sawtooth spectrum, 3 for positive frequency and 3 others for negatives ones. ) | ||
* in a real system, bandpass filtering before demodulation is used. As will be shown, the lowpass filter is equivalent to a bandpass filter acting on the | * in a real system, bandpass filtering before demodulation is used. As will be shown, the lowpass filter is equivalent to a bandpass filter acting on the passband modulated signal | ||
* Only taking magnitude is a good AM demodulation since it is less sensitive to frequency and phase lack of synchronism found in real systems. | * Only taking magnitude is a good AM demodulation since it is less sensitive to frequency and phase lack of synchronism found in real systems. | ||
|} | |} | ||
| Line 289: | Line 290: | ||
* this transceiver can be used to generate and transmit any modern digital communications like OOK, ASK, PSK, and QAM depending on choosen signal ''i(t)'' and ''q(t)'' | * this transceiver can be used to generate and transmit any modern digital communications like OOK, ASK, PSK, and QAM depending on choosen signal ''i(t)'' and ''q(t)'' | ||
* quantities with an hat like <math>\hat{i}(t)</math> should be similar or equal to corresponding <math>i(t)</math> | * quantities with an hat like <math>\hat{i}(t)</math> should be similar or equal to corresponding <math>i(t)</math> | ||
* signal ''i(t)'' and ''q(t)'' are generated using Dirac impulse | * signal ''i(t)'' and ''q(t)'' are generated using Dirac impulse weighted by amplitudes ''a<sub>k</sub>'' and ''b<sub>k</sub>'' and a shaping filter ''h<sub>1</sub>(t)'' | ||
* the considered channel is | * the considered channel is Additive White Gaussian Noise (AWGN) | ||
* | * IQ modulator and IQ demodulator are not necessarily synchronized | ||
* Baseband filter are used to limit the bandwidth in the emitter and limit noise in the receiver. In a well construct Transceiver chain, ''h<sub>1</sub>(t)'' and ''h<sub>3</sub>(t)'' should be Root Nyquist filters | * Baseband filter are used to limit the bandwidth in the emitter and limit noise in the receiver. In a well construct Transceiver chain, ''h<sub>1</sub>(t)'' and ''h<sub>3</sub>(t)'' should be Root Nyquist filters | ||
* A Bandpass filter is used in the channel, it can represent the channel effect as well as any additional filter used on the modulated signal | * A Bandpass filter is used in the channel, it can represent the channel effect as well as any additional filter used on the modulated signal | ||
| Line 305: | Line 306: | ||
** This result from section [[#complex_envelope_of_a_pure_sine_wave| complex envelope of a pure sine wave]] | ** This result from section [[#complex_envelope_of_a_pure_sine_wave| complex envelope of a pure sine wave]] | ||
* Replace any bandpass filter by its equivalent baseband complex filter as defined below | * Replace any bandpass filter by its equivalent baseband complex filter as defined below | ||
* Replace channel | * Replace channel passband noise by its equivalent baseband complex noise as defined below | ||
=== Bandpass filter=== | === Bandpass filter=== | ||
[[File:IQ_complex_tutorial_complex_filter.png|thumb|500px||Equivalent baseband filter of a bandpass filter]] | [[File:IQ_complex_tutorial_complex_filter.png|thumb|500px||Equivalent baseband filter of a bandpass filter]] | ||
Any bandpass filter with frequency | Any bandpass filter with frequency transfer function <math>H(f)</math> having a limited bandwidth can be represented by an equivalent baseband filter <math>H^{bb}(f)</math> . The baseband filter frequency transfer is the positive part of the transfer function shifted toward 0 (same process as above for AM Spectrum) | ||
: <math>H^{bb}(f)=H^+(f+F_0)</math> | : <math>H^{bb}(f)=H^+(f+F_0)</math> | ||
So we observe that the equivalent filter is a lowpass filter. | So we observe that the equivalent filter is a lowpass filter. | ||
As <math>H(f)</math> is not necessarily symmetric around ''F<sub>0</sub>'', <math>H^{bb}(f</math> can be unsymmetric: this correspond to a complex time | As <math>H(f)</math> is not necessarily symmetric around ''F<sub>0</sub>'', <math>H^{bb}(f)</math> can be unsymmetric: this correspond to a complex time transfer function, what we will call a complex filter. | ||
So the baseband equivalent of a band pass filter is a complex filter acting on a complex signal. | So the baseband equivalent of a band pass filter is a complex filter acting on a complex signal. | ||
| Line 329: | Line 330: | ||
=== Channel noise === | === Channel noise === | ||
Any | Any passband noise <math>N(t)</math> having a limited bandwidth can be represented by an equivalent baseband noise <math>N^{bb}(t)</math> . The baseband equivalent noise spectrum is the positive part of the passband noise spectrum shifted toward 0 (same process as above for AM Spectrum and for filter) | ||
: <math>N^{bb}(f)=N^+(f+F_0)</math> | : <math>N^{bb}(f)=N^+(f+F_0)</math> | ||
| Line 357: | Line 358: | ||
|} | |} | ||
Open [[Media:IQ_tutorial_QPSK_TX_RX.grc|IQ_tutorial_QPSK_TX_RX.grc]]. Note that BPSK constellation block | Open [[Media:IQ_tutorial_QPSK_TX_RX.grc|IQ_tutorial_QPSK_TX_RX.grc]]. Note that BPSK constellation block is connected before the multiplier, while BPSK spectrum is evaluated after the multiplier. | ||
* Simulate the flowgraph. Adjust ''Delta_f (BPSK shift)'' to 0. Observe the constellation and the spectrum of both signals | * Simulate the flowgraph. Adjust ''Delta_f (BPSK shift)'' to 0. Observe the constellation and the spectrum of both signals | ||
* Increase noise level, observe the complex noise on BPSK and QPSK constellation | * Increase noise level, observe the complex noise on BPSK and QPSK constellation | ||
| Line 377: | Line 378: | ||
=== GNURadio XLating filter === | === GNURadio XLating filter === | ||
[[File:IQ_tutorial_QPSK_TX_RX_2.png|thumb|800px|Basic Tx/Rx using a Xlating filter at receiver]] | [[File:IQ_tutorial_QPSK_TX_RX_2.png|thumb|800px|Basic Tx/Rx using a Xlating filter at receiver]] | ||
GNURadio XLating filter perform | GNURadio XLating filter can perform the following actions | ||
* | * It can shift the spectrum in the frequency domain | ||
* | * It can filter the result with the specified filter | ||
* | * It can decimate the signal | ||
The Xlating filter is | The Xlating filter is useful every time a signal spectrum is not centered, and/or when you need to select one signal in a spectrum where several channel are in use. | ||
Open [[Media:IQ_tutorial_QPSK_TX_RX_2.grc|IQ_tutorial_QPSK_TX_RX_2.grc]]. | Open [[Media:IQ_tutorial_QPSK_TX_RX_2.grc|IQ_tutorial_QPSK_TX_RX_2.grc]]. | ||
Latest revision as of 09:37, 16 August 2023
This tutorial originates from discussions on discuss-gnuradio@gnu.org. We will explain why simulating digital communications requires equivalent baseband representation of signals--which in fact are complex signals. For this reason, complex signals are essential in GNURadio.
This tutorial is also intended for non-specialists, as it involves as little maths as possible while presenting most results using GNURadio's flowgraph. Some examples involving simple modulation schemes used in HAM radio are presented. While introducing complex signals can be seen as increasing complexity, we will see that it drastically simplifies the understanding of certain concepts, such as synchronization.
If you are searching for more detailed information, please refer to the literature--such as references [1],[2],[3].
Some maths
This section summarizes complex number properties used in this tutorial. More information can be found on complex number Wikipedia page.
A complex number is a number of the form a + jb, where a and b are real numbers, and j is an indeterminate satisfying j2=-1 (Mathematician prefer using i instead of j used by physicist and radio engineers). For example, z1=2 + j3 is a complex number. The real part Re{z} of z1 is 2 and its imaginary part Im{z} is 3.
Complex numbers can be represented in the complex plane as vectors. The modulus or magnitude r of a complex number z = a + jb is
The phase φ of z (referred to as the argument) is the angle of the radial Oz on the positive real axis.
- (for a≠0)
Together, r and φ provide another means of representing complex numbers--both the polar and exponential forms.
The exponential form is convenient for computing the multiplication of two complex numbers.
The following complex numbers have a unit magnitude r=1 :
A complex signal c(t) can be seen as two real signals a(t), b(t)--often written as i(t), q(t)--and combined to create a complex signal. It can also be represented by its amplitude over time r(t) as well as its phase variation over time φ(t)
Why we need complex and IQ signals
GNURadio software is mainly used to design and study radio communications. Making high frequency transmission requires modulating a high frequency carrier of frequency f0. The most common modulation for analog transmissions are: amplitude modulation (AM), phase modulation (PM), and frequency modulation (FM).
For analog AM, the modulated signal m(t) is simply the mathematical product of the carrier c(t) and the baseband signal a(t). The corresponding hardware is a mixer whose scheme and mathematical representation is a multiplier.
We call a(t) a baseband signal since its spectrum is in a low frequency range--starting near 0 Hz (e.g. [0-20kHz] for a HiFi audio signal).
The spectrum of an AM modulated signal M(f) is the translation of the audio spectrum A(f) around ±F0 with A(f) being the entire spectrum of the modulating signal, using both positive and negative frequencies
Important - Negative frequencies are often omitted in spectrum representation since, for real signal (a(t), m(t) are real) the power spectrum are symmetric around zero (more details on this later).
Up to now we have been dealing with real signals. The need for complex signals appears in the next step. Simulation requires sampled signal. Sampling is the operation of observing a continuous signal and taking a finite number of samples at a given sampling rate fs (i.e. one sample each 1/fs second). Because a simulator can only make calculations on a finite number of samples, it requires a sampled signal. Nyquist Sampling theorem states that the sampling rate must be greater than twice the maximum frequency FMax in order to reconstruct the original signal from the sampled signal.
For a HiFi audio signal, the maximum audio frequency is close to 20 kHz, so the sampling rate must be higher than 40 kHz (44.1 kHz is often used in computer sound cards, 8 kHz is used for mobile phones since voice has a lower frequency range than HiFi audio).
For an AM signal modulated by an audio signal, the maximum frequency of the modulated spectrum is . Direct sampling of such a signal is not possible with conventional hardware such as a low cost SDR dongle. If the carrier frequency is close to 1 GHz, the sampling rate should be at least 2 GHz. This is obviously too much for the computer to handle (higher than some CPU clocks).
Flowgraph IQ_tutorial_AM_TX_real.grc illustrates amplitude modulation using only real blocks (excepted for bits source). As a consequence, the maximum carrier frequency is limited to several tens of kHz.
- study the modulator part which simply multiplies the baseband signal and the sinusoidal carrier
- look at the influence of the carrier frequency on the modulated signal spectrum (carrier frequency must stay lower than half the sampling rate)
- look at the spectrum shape for sawtooth input and random bit sequence (QT GUI chooser and selector)
- When transmitting random bits, you can deactivate the interpolating FIR Filter and replace it by a root raised cosine filter
Spectral properties of signals
Amplitude spectrum is calculated using the Fourier Transform. It represents how the power is spread in the frequency domain. It allows for determining the signal bandwidth. Power Spectral Density or PSD correspond to the average magnitude of the Amplitude spectrum.
In this section we summarize some properties of the phase arg{X(f)} and magnitude |X(f)|. We first consider properties for continuous signal. Then we will investigate additional properties of sampled signal (those used in GNURadio).
Given a signal x(t) its amplitude/phase spectrum is denoted X(f) which is a complex function given by :
continuous real signal
Every real signal has a spectrum whose magnitude is symmetric and phase is anti-symmetric.
continuous complex signal
The main difference with real signal is that:
- any complex signal having non null imaginary part exhibits a non-symmetric spectrum.
- as a consequence, every non-symmetric spectrum corresponds to a complex signal
sampled signals
We consider a signal x(t) and we note its sampled version xs(t) sampled at frequency Fs.
The spectrum Xs(f) of the sampled signal is a periodic function of period Fs.
So the sampled signal spectrum verify :
Generally the bandwidth of X(f) is lower then Fs/2. The infinite sum defined above exhibit no aliasing (no superposition of patterns X(f), X(f+Fs) and X(f-Fs)). In that case, as stated in the Nyquist theorem of sampling, the original spectrum/signal can be recovered by filtering the sampled signal.
When the maximum frequency of the signal spectrum do not respect Nyquist theorem, one should filter the signal with a low pass filter having a cutt-off frequency lower then Fs/2 before sampling: this correspond to the anti-aliasing filter used in every SDR hardware.
Complex envelope, equivalent baseband signal
Baseband signals have a spectrum at low frequency near 0 Hz. Audio, video and NRZ line code are baseband signals.
Passband signals have no energy near 0 Hz and a spectrum located near a high frequency (generally the carrier frequency). Analog and digital AM, PM and FM modulated signals are passband signals.
A theorem ([1],[2],[3]) states that any high frequency passband signal having a limited bandwidth B can be represented by a baseband equivalent signal having the same bandwidth. This baseband equivalent signal also called the complex envelope is used in simulators since it allows to lower sampling rate as compared to directly sampling the passband signal.
The equivalent baseband representation helps us for the simulation of passband signals. At this step we need some math. We will consider a carrier modulated in phase and/or amplitude (in the sake of simplicity, Frequency modulation is not considered but it can be related to phase modulation.). Such a modulated signal m(t) and it's complex representation is :
For modulated signal, the complex representation is obtained by replacing the cos function by an exponent function . For a more general definition see [1],[2],[3] . The real signal corresponds to the real part of the complex signal .
One important property of spectrum is that it has only energy in the positive frequency range and verify.
where denotes the restriction of to the positive frequency range.
Let us now look at the complex envelope or equivalent baseband signal of passband signal defined by :
Multiplying a signal by correspond to a frequency translation of the spectrum so that we have:
So the spectrum of the complex envelope is a baseband signal whose spectrum has the same shape as . For this reason, knowing or is sufficient to reconstruct or .
Equivalent baseband, Envelope, Complex signals?
Terms equivalent baseband signal, complex envelope and complex signal can be seen as equivalent terms referring to the same thing.
While simulating some radio we have mainly two type of signals:
- any low frequency or baseband signal are real signal, they are represented by real signals
- every passband signal must be represented by their equivalent baseband complex signal (excepted for systems having very low carrier frequency)
So in a gnuradio flowgraph, there is no ambiguity: every complex signal (blue interconnections) is implicitly an equivalent representation of a passband signal so we will simply call it a complex signal.
IQ modulator and demodulator
Let us now come to hardware and SDR and first rewrite the equivalent baseband signal and the modulated signal m(t) :
The phase φ(t) of the modulated signal m(t), is identical to the phase of the complex signal c(t)=i(t)+jq(t). The equivalent baseband signal c(t) is represented in a complex plane also refeered to as the IQ plane. The resulting m(t) can be any modulated in AM, PM or even FM signal.
As a result, the modulated signal m(t) is the addition of :
- which is an AM modulated signal, the product of i(t) by a signal In phase with the carrier (i stand for In phase)
- which is an AM modulated signal, the product of q(t) by a signal in Quadrature with the carrier (q stand for Quadrature)
The corresponding hardware is called an IQ modulator. Every modern radio communication uses IQ modulator for emitting and IQ demodulator for receiving. The IQ demodulator is able to recover incoming i(t) and q(t). If the amplitude of the recovered carrier is 2, and if modulator and demodulator carrier are synchronous (same frequency and phase) the output of the IQ demodulator correspond to input i(t) and q(t).
In real hardware, carrier are not synchronous and the receiver must compensate any phase and frequency difference between emitter and receiver. This is done using some hardware and/or software such as polyphase clock sync, and Costas loop.
SDR Module such as USRP (USRP N320 block Diagram) and SDR Dongle (RTL-2832) input and output are the 2 real signals i(t) and q(t) combined to form the complex signal i(t) + j q(t) which turns to be the equivalent baseband of the modulated emitted or received signal. These hardware are based on IQ modulator and IQ demodulator associated with mixers when intermediate frequency (IF) is used.
Some examples of EqBB signals
In order to get familiar with complex signal, let us consider some basic examples.
First, we suppose our emitter carrier is so that every equivalent baseband signal will be defined according to this reference.
complex envelope of a pure sine wave
We will consider a pure sine wave, close to the carrier having a Δf frequency shift and φ phase shift as compared to the carrier. After some math we get its complex equivalent signal.
The complex envelope of the carrier itself is found for Δf=0 and φ=0 which yields . We conclude that in a GNURadio flowgraph, the carrier is represented by a continuous components, a pure DC signal ; this may seem counter intuitive. The spectrum is a single peak at f=0 which can be represented using the Dirac δ(f) function (or distribution) : . Shifting this spectrum of towards positive frequency we get the positive part of the carrier spectrum (a peak at ) : . The negative part of the spectrum is simply obtained by symmetry of the real part (a peak at ).
This can be simulated with GNURadio flowgraph IQ_tutorial_eq_bb.grc. The spectrum of our carrier is centered at 0 Hz. The Frequency sink has a feature to shift this spectrum around which is a parameter of the sink. In a simulation, it is not necessary to represent the negative part of the spectrum since m(t) being real, it spectrum is obviously symmetric.
We will now consider Δf ≠0 which simulate a signal not exactly synchronous to the carrier. This yields
The complex envelope is rotating vector (you can simulate this with Δf=1 Hz giving a vector which rotate at 60 rpm or 1 turn per second) , its spectrum is a single peak at f=+Δf. This complex signal exhibits a non symmetric spectrum (no peak at f=-Δf). Change Δf to -0.5 Hz, the vector now rotates counter clockwise at 30 rpm or 0.5 turn per second.
Exercise: Open flowgraph IQ_tutorial_eq_bb.grc. Parameter delta_f is set with an increment of 1/12, which correspond to 5 rotation per minute.
- For Δf=1/12=0.0833, what is the speed of rotation of the complex signal?
- What do you observe when Δf=-1/12=-0.0833 ?
- Slowly increase Δf to reach fs/2 and observe the spectrum really has a single peak at Δf. Explain your observation when Δf>fs/2'.
- Do the same for a negative Δf
- For Δf =fs what is the equivelant baseband frequency. What is the carrier frequency ?
- Set Δf=0 and φ≠0. Discuss the simulated equivalent baseband signal.
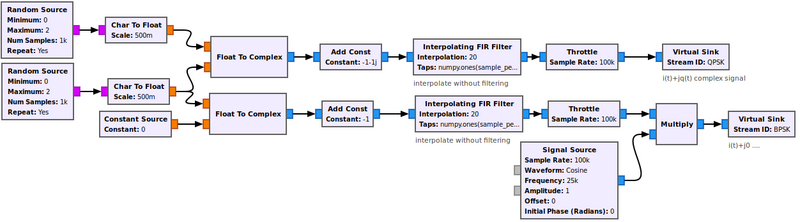
AM mod demod example
This example will consider signal baseband signal a(t) modulating a carrier at F0 in AM, and its demodulation. As no phase modulation in used, φ(t)=0 and consequently q(t)=0.
AM modulation is a special case for which the equivalent baseband complex signal has a null imaginary part and is real. Considering the schematic diagram of an IQ modulator demodulator, when q(t)) is null the diagram is simplified (imaginary path is not used) yielding the well known AM modulation/demodulation scheme.
Remind that in GNURadio flowgraph :
- orange connections correspond to real signals (float numbers)
- blue connections correspond to complex signals (complex numbers)
Flowgraph IQ_tutorial_AM_TX_complex.grc contains two equivalent diagram for an AM modulation with a sawtooth input:
- the upper one uses real signals. It is the exact AM modulator uses at the beginning of this tutorial.
- sampling frequency is 200 kHz, 40 times the input rate which equal 5 kHz.
- allowing a maximum carrier frequency close to 100kHz
- the lower one uses an equivalent baseband representation.
- sampling frequency is 25 kHz, 5 times the input rate which equal 5 kHz.
- the sawtoooth correspond to identical generator in both modulator
- each blue input or output is the baseband equivalent of the corresponding signal in the upper AM modulator.
- the carrier frequency can be any value compatible with connected Hardware
- the carrier equivalent signal equal 1 (as stated in the previous section) so it has been disable and replaced by a complex constant
- the Hardware input is the complex equivalent baseband signal
- the carrier frequency is not needed nor used in complex blocks; excepted in the QT GUI spectrum to label the center frequency which is 0 but correspond to the F>sub>0.
Three blocks are unusefull and can be removed from the lower complex modulator:
- save the current flowgraph as IQ_tutorial_AM_TX_complex_2.grc.
- remove the complex multiplier, the carrier equivalent baseband (complex constant=1) and the carrier complex source (the disabled one). Reconnect complex to float and throttle blocks to obtain the flowgraph sketched on the right.
You can now run this flowgraph and compare signal and their spectrum in both modulator. Once again, these simulations suppose perfectly synchronous emitter and receiver carrier which is quite far from reality.
Further work : construct the AM demodulator flowgraph
Use the flowgraph IQ_tutorial_AM_TX_complex_2.grc that you created, add blocks to perform AM demodulation and to recover the input signal a(t) from the modulated signal. You have to use the equivalent baseband representation of the demodulator.
| 1st indication |
| Remind and use the relation between a(t) and c(t)=i(t)+jq(t) given above. |
| 2nd indication |
| An AM demodulator extract the amplitude (magnitude) of the modulated signal... |
| Solution including filter |
| IQ_tutorial_AM_TX_complex_3.grc
Running this flowgraph, demodulation is obtained taking the real part (imperfect solution), or the magnitude (good solution) of the complex signal.
|
QPSK example
QPSK digital signal exhibit four phase state .
And the baseband equivalent signal also exhibit 4 different values each one being used to code a 2 bits sequence 00 01 10 or 11 :
Normally, we would use a GNURadio "constellation modulator" to simulate QPSK as is done in the excellent Guided Tutorial on PSK Demodulation.
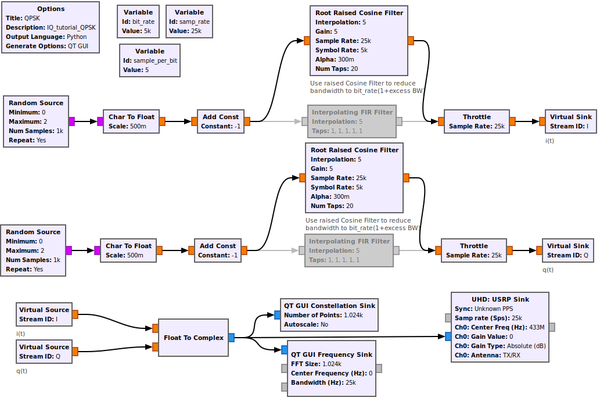
For the present tutorial we will simulate a QPSK without Nyquist filter in order to get phase states which can be simply displayed on a constellation sink. This is not possible with constellation modulator. Our QPSK modulator (complex representation) is build taking into account that the complex signal exhibit 4 different values, its obvious that both i(t) and q(t) have only 2 states so they are binary symmetric NRZ line codes:
Flowgraph IQ_tutorial_QPSK.grc generates 2 sequences of bits, interpolates them to get 2 binary symmetric NRZ line codes. The NRZ signals are combined to create the complex equivalent baseband signal of the QPSK which can be transmitted to any SDR emitter.
Simulate this flowgraph :
- stop the QT GUI spectrum to observe that the complex baseband signal spectrum is no longer symmetric as expected for complex signals.
- use spectrum averaging to see that despite of the previous observation, the power spectral density (average of the magnitude spectrum) is symmetric around 0 (which correspond to F0 for the modulated signal.
- Disable the interpolating filters and enable both root raised cosine filter (the filter used in every QPSK emitter). This yields the real spectrum of a QPSK.
Equivalent baseband representation
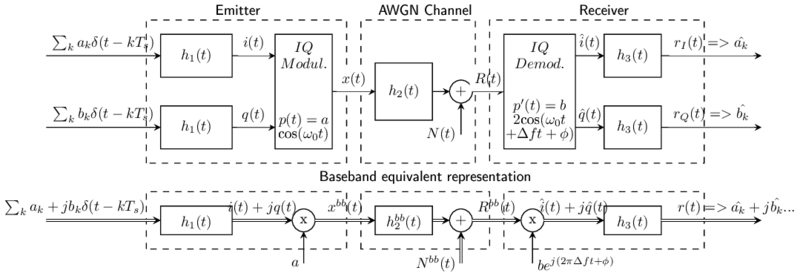
This diagram sketch a classical Emitter/Receiver (Tx/Rx) transmission including channel noise, and its equivalent baseband representation which could be used for a GNURadio simulation.
- this transceiver can be used to generate and transmit any modern digital communications like OOK, ASK, PSK, and QAM depending on choosen signal i(t) and q(t)
- quantities with an hat like should be similar or equal to corresponding
- signal i(t) and q(t) are generated using Dirac impulse weighted by amplitudes ak and bk and a shaping filter h1(t)
- the considered channel is Additive White Gaussian Noise (AWGN)
- IQ modulator and IQ demodulator are not necessarily synchronized
- Baseband filter are used to limit the bandwidth in the emitter and limit noise in the receiver. In a well construct Transceiver chain, h1(t) and h3(t) should be Root Nyquist filters
- A Bandpass filter is used in the channel, it can represent the channel effect as well as any additional filter used on the modulated signal
One may observe that this transceiver don't include non linear effect suchs as amplifier intermodulation. In fact, complex baseband representation don't permit precise modelization of non linear effects so they are not considered here. Complex signals on the baseband equivalent representation are represented using double arrow.
Every linear band limited system has an equivalent baseband which is build using the following rules.
- Replace IQ modulator inputs i(t) and q(t) by a complex signal i(t) + jq(t)
- Similarly replace IQ demodulator outputs by a complex signal
- Keep any baseband filter acting on baseband signal unchanged (filter h1(t) is acting on i(t) and q(t) so it can be replaced by a single filter acting on complex signal i(t) + jq(t). However one could have used two identical filters each acting on one real signal)
- Replace IQ modulator by a multiplication by a (the modulator carrier is used as a reference to define complex equivalent baseband, no multiplier if a=1)
- Replace IQ demodulator by a multiplication by (no multiplier if b=1 and demodulator is synchronized to modulator
- This result from section complex envelope of a pure sine wave
- Replace any bandpass filter by its equivalent baseband complex filter as defined below
- Replace channel passband noise by its equivalent baseband complex noise as defined below
Bandpass filter
Any bandpass filter with frequency transfer function having a limited bandwidth can be represented by an equivalent baseband filter . The baseband filter frequency transfer is the positive part of the transfer function shifted toward 0 (same process as above for AM Spectrum)
So we observe that the equivalent filter is a lowpass filter.
As is not necessarily symmetric around F0, can be unsymmetric: this correspond to a complex time transfer function, what we will call a complex filter.
So the baseband equivalent of a band pass filter is a complex filter acting on a complex signal.
Normally, when filtering complex signal in GNURadio, in most situation complex taps must be used. In case your baseband filter is symmetric around F0 it turns to be a real filter, it can be represented using real taps.
Unsynchronized demodulator
For a receiver carrier p'(t) given by
It is found that the equivalent baseband is a multiplication with
Which is similar (excepted for a factor 2) to the result given for the baseband equivalent of a pure sine wave close to the carrier. The factor 2 difference come from the demodulation process.
Channel noise
Any passband noise having a limited bandwidth can be represented by an equivalent baseband noise . The baseband equivalent noise spectrum is the positive part of the passband noise spectrum shifted toward 0 (same process as above for AM Spectrum and for filter)
So we find that the baseband equivalent noise is a low frequency noise. Furthermore, as for filters, the baseband equivalent noise is complex, its real part and imaginary part having the same variance (power).
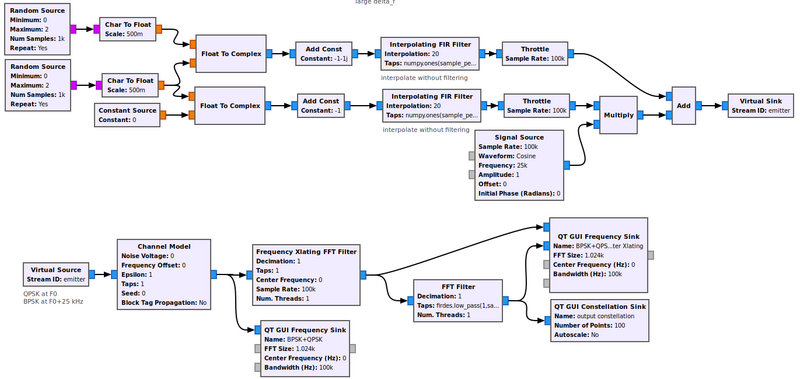
Tx/Rx PSK equivalent baseband simulation
In this section we will illustrate equivalent baseband blocks introduced above:
- complex noise
- complex filters
- IQ demodulator with carrier asynchronism,
This will be done using a simple QPSK and BPSK transceiver simulation. We will not really investigate demodulation but concentrate on what should be done to compensate for the channel impairments.
Let us first examine this flowgraph. The upper part of the flowgraph generate a QPSK signal as used in a previous flowgraph. The lower part is a modified version of the first one.
Questions :
- If we do not account for the multiplier, what type of signal will generate the second part of this flowgraph (at the throttle output)?
- What is the effect the multiplier (source is at 25 Khz which is 1/4 of the sampling rate) ?
| Solution |
| the second signal is a BPSK (i(t) is an NRZ Line code, q(t) is 0. The two phase states of this BPSK are 0° and 180°. |
| Without multiplier this BPSK would be centered at F0. As it is multiplied by a complex exponent at 25 kHz, it will be shift at F0+ 25 kHz |
Open IQ_tutorial_QPSK_TX_RX.grc. Note that BPSK constellation block is connected before the multiplier, while BPSK spectrum is evaluated after the multiplier.
- Simulate the flowgraph. Adjust Delta_f (BPSK shift) to 0. Observe the constellation and the spectrum of both signals
- Increase noise level, observe the complex noise on BPSK and QPSK constellation
- Change Delta_f (BPSK shift) and observe how the BPSK Spectrum is shifted.
- What is the BPSK center frequency ?
- Explain why the BPSK constellation in this case is rotating
We will now investigate the channel frequency offset parameter. This parameter is used to simulate the frequency offset between a receiver and an emitter.
Stop the simulation. Disable delta_f_over_fs QT Gui range and enabled the one which was disabled (larger range) and run the flowgraph.
- select the spectrum tab, and increase Delta_f (BPSK shift) to 25 kHz
- change delta_f_over_fs value and observe how it shifts the spectrum of the received signal the same way as our multiplier does.
Let's suppose we receive a modulated at the output of an unsynchronized receiver (hardware). Let's suppose that we have measured the carrier frequency difference between emitter end receiver. The modulated signal spectrum is not centered around F0. There is several way to compensate for this effect:
- Specify a receiver frequency which compensate the frequency difference (most SDR Source in GNURadio can specify a frequency shift which is given in PPM (Parts per million).
- Multiply the received signal by
- Use a GNURadio Xlating filter block which perform the previous multiplication and a filtering.
GNURadio XLating filter
GNURadio XLating filter can perform the following actions
- It can shift the spectrum in the frequency domain
- It can filter the result with the specified filter
- It can decimate the signal
The Xlating filter is useful every time a signal spectrum is not centered, and/or when you need to select one signal in a spectrum where several channel are in use.
Open IQ_tutorial_QPSK_TX_RX_2.grc.
This flowgraph
- generate a single signal composed of:
- our QPSK signal at F0
- the BPSK signal at F0+25 kHz
- simulate a channel frequency offset
- use a Xlating filter to shift the received signal (compensate the channel and/or select the desired channel)
- filter the signal to select only one signal BPSK or QPSK (low pass with 12 kHz cutt-off frequency)
- note: filtering is performed after Xlating so thaht we can display filtered and unfiltered signals on the same spectrum.
- display the constellation of the demodulated channel (constellation are now different from a perfect constellation , this is due to the low pass filter.
Simulate this flowgraph. By default the QPSK signal is demodulated.
- observe that the constellation is close to the QPSK one (excepted for filter effect, at this point we should use Nyquist filters to recover the QPSK constellation)
- Slowly increase Xlating filter frequency offset and observe the spectrum shift
- Select the Xlating filter frequency offset to demodulate the BPSK (25kHz) and observe how it is uneasy or impossible to get a correct constellation.
- You should get approximately 2 set of points, but these point are shift as compared to the perfect BPSK constellation. This is normal, we compensate frequency while in a real receiver it is necessary to compensate both frequency and phase shift
- In fact simulating a delta_f frequency which change during simulation is equivalent to having a phase and a frequency shift.
Asynchronism in real hardware
The above simulation have explained the basis of asynchronism found in any hardware Tx/Rx and some basic method to recover synchronism.
However keep in mind that dealing with real hardware is more complicated then described here. The frequency and phase shift between emitter and receiver should be considered as dynamic and changing continously and randomly with time.
As a consequence, we need more robust block to continuously synchronize emitter and receiver. Fortunately, digital signal processing offer many solutions to these impairments. Curious reader are encouraged to read the excellent GNURadio Guided Tutorial on PSK Demodulation.
References
Further reading for complex equivalent baseband signal:
- [1] Proakis J., Digital Communication, McGraw Hill Series in Electrical and Computer Engineering, Singapore, 1989
- [2] Gallager R., Principles of digital communication, Cambridge University Press Cambridge, UK, 2008
- [3] Benedetto S. and Biglieri E., Principles of digital transmission : with wireless applications, Kluwer Academic/Plenum Publishers, NY, 1999
About figures
Most figures were generated from .grc flowgraph referenced in the text, and from .odg and .tex file. For completeness, these files are included in the following compressed archive IQ_complex_tutorial_files.zip.grc so that anyone can easily improve this tutorial. If you modify some figure, please update this archive too.
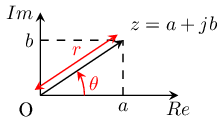






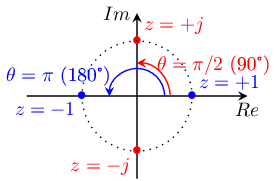




































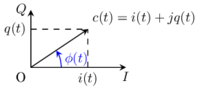

![{\displaystyle m(t)={\text{Re}}\left[{\big (}i(t)+jq(t){\big )}e^{j2\pi F_{0}t}\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bbfb1dabf2f6e18dd0c93c8b2f20ba6e43bae6de)