LDPC Encoder Definition (via Parity Check): Difference between revisions
(Created page with "Category:Block Docs Category:Stub Docs This is the template for the "Page-per-block Docs". This first section should describe what the block...") |
|||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Block Docs]] | [[Category:Block Docs]] | ||
This block creates a LDPC Encoder Definition variable. | |||
This | |||
This encoder performs a reduced complexity algorithm described by Richardson and Urbanke in Appendix A of their book: Modern Coding Theory. Compared to the block [[LDPC Encoder Definition (via Generator)]], this encoder requires orders of magnitude fewer operations to create each codeword. This is accomplished by completing a significant amount of the complex matrix manipulation (including inverse, multiplication, and Gaussian elimination operations) during preprocessing. The disadvantage of this encoder is that it requires a specially formatted matrix. However, GNU Radio includes python scripts to format a standard parity check matrix appropriately for this encoder, as well as a small library of encoding-ready matrices for use. | |||
== Parameters == | == Parameters == | ||
; | ; Parallelism | ||
: | : For parallel execution of multiple instances of the block (more info is needed on this) | ||
; | ; Dimension 1 | ||
: | : For parallelism | ||
; Dimension 2 | |||
: For parallelism | |||
; Parity check matrix | |||
: The specific format of this parity check matrix is described by Richardson and Urbanke in Appendix A of their book: Modern Coding Theory (ISBN 978-0-521-85229-6). The matrix can be loaded by creating a [https://wiki.gnuradio.org/index.php/LDPC_Parity_Check_Matrix LDPC Parity Check Matrix] block and using its Id in this field. | |||
== Example Flowgraph == | == Example Flowgraph == | ||
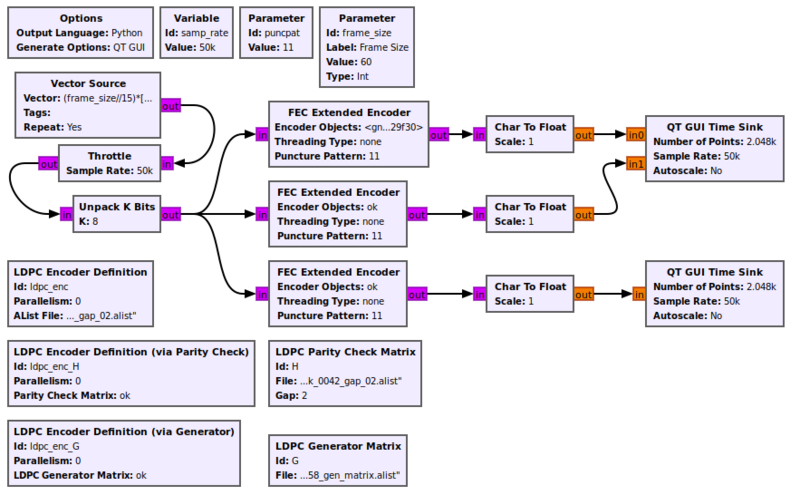
This flowgraph can be found at [https://github.com/gnuradio/gnuradio/blob/master/gr-fec/examples/fecapi_ldpc_encoders.grc] | |||
[[File:Fecapi_ldpc_encoders_fg.png|800px]] | |||
== Source Files == | == Source Files == | ||
; C++ files | ; C++ files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-fec/lib/ldpc_par_mtrx_encoder_impl.cc ldpc_par_mtrx_encoder_impl.cc] | ||
; Header files | ; Header files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-fec/lib/ldpc_par_mtrx_encoder_impl.h ldpc_par_mtrx_encoder_impl.h] | ||
; Public header files | ; Public header files | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-fec/include/gnuradio/fec/ldpc_par_mtrx_encoder.h ldpc_par_mtrx_encoder.h] | ||
; Block definition | ; Block definition | ||
: [https://github.com/gnuradio/gnuradio | : [https://github.com/gnuradio/gnuradio/blob/main/gr-fec/grc/variable_ldpc_encoder_H.block.yml variable_ldpc_encoder_H.block.yml] | ||
Latest revision as of 10:53, 7 June 2022
This block creates a LDPC Encoder Definition variable.
This encoder performs a reduced complexity algorithm described by Richardson and Urbanke in Appendix A of their book: Modern Coding Theory. Compared to the block LDPC Encoder Definition (via Generator), this encoder requires orders of magnitude fewer operations to create each codeword. This is accomplished by completing a significant amount of the complex matrix manipulation (including inverse, multiplication, and Gaussian elimination operations) during preprocessing. The disadvantage of this encoder is that it requires a specially formatted matrix. However, GNU Radio includes python scripts to format a standard parity check matrix appropriately for this encoder, as well as a small library of encoding-ready matrices for use.
Parameters
- Parallelism
- For parallel execution of multiple instances of the block (more info is needed on this)
- Dimension 1
- For parallelism
- Dimension 2
- For parallelism
- Parity check matrix
- The specific format of this parity check matrix is described by Richardson and Urbanke in Appendix A of their book: Modern Coding Theory (ISBN 978-0-521-85229-6). The matrix can be loaded by creating a LDPC Parity Check Matrix block and using its Id in this field.
Example Flowgraph
This flowgraph can be found at [1]
Source Files
- C++ files
- ldpc_par_mtrx_encoder_impl.cc
- Header files
- ldpc_par_mtrx_encoder_impl.h
- Public header files
- ldpc_par_mtrx_encoder.h
- Block definition
- variable_ldpc_encoder_H.block.yml