OFDM Serializer: Difference between revisions
No edit summary |
|||
| Line 36: | Line 36: | ||
== Example Flowgraph == | == Example Flowgraph == | ||
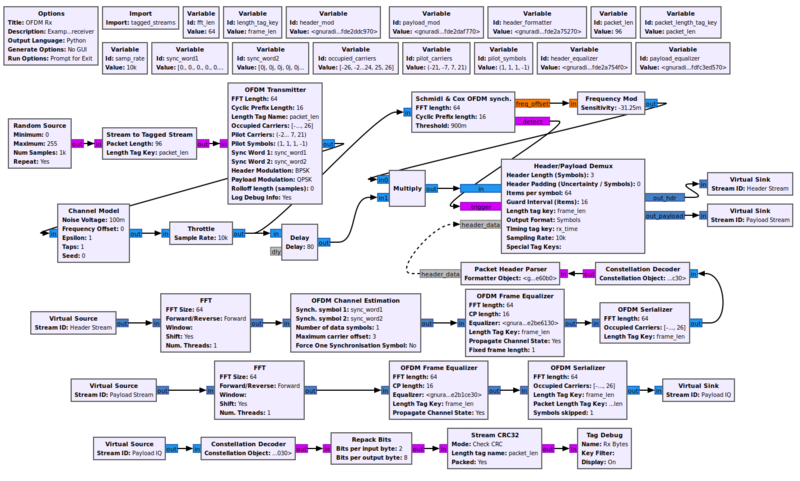
This flowgraph can be found at [https://github.com/gnuradio/gnuradio/blob/master/gr-digital/examples/ofdm/rx_ofdm.grc]. | |||
[[File:Rx_ofdm_fg.png|800px]] | |||
== Source Files == | == Source Files == | ||
Revision as of 02:43, 30 November 2020
Serializes complex modulations symbols from OFDM sub-carriers.
This is the inverse block to the OFDM Carrier Allocator. It outputs the complex data symbols as a tagged stream, discarding the pilot symbols.
If given, two different tags are parsed: The first key () specifies the number of OFDM symbols in the frame at the input. The second key () specifies the number of complex symbols that are coded into this frame. If given, this second key is then used at the output, otherwise, is used. If both are given, the packet length specifies the maximum number of output items, and the frame length specifies the exact number of consumed input items.
It is possible to correct a carrier offset in this function by passing another tag with said offset.
- Input
- Complex vectors of length
- Output
- Complex scalars, in the same order as specified in occupied_carriers.
Parameters
- FFT length
- FFT length
- Occupied Carriers
- See OFDM Carrier Allocator
- Length Tag Key
- The key of the tag identifying the length of the input frame in OFDM symbols.
- Packet Length Tag Key
- The key of the tag identifying the number of complex symbols in this packet.
- Symbols skipped
- If the first symbol is not allocated as in occupied_carriers[0], set this
- Carrier Offset Key
- When this block should correct a carrier offset, specify the tag key of the offset here (not necessary if following an ofdm_frame_equalizer_vcvc)
- Input is shifted
- If the input has the DC carrier on index 0 (i.e. it is not FFT shifted), set this to false
Example Flowgraph
This flowgraph can be found at [1].
Source Files
- C++ files
- [2]
- Header files
- [3]
- Public header files
- [4]
- Block definition
- [5]