Schmidl & Cox OFDM synch.

Schmidl & Cox synchronisation for OFDM.

Input

complex samples.

Output 0

Fine frequency offset, scaled by the OFDM symbol duration. This is ${\hat {\varphi }}$ in [1]. The normalized frequency offset is then 2.0*output0/fft_len.

Output 1

Beginning of the first OFDM symbol after the first (doubled) OFDM symbol. The beginning is marked with a 1 (it's 0 everywhere else).

The evaluation of the coarse frequency offset is not done in this block. Also, the initial equalizer taps are not calculated here.

Note that we use a different normalization factor in the timing metric than the authors do in their original work[1]. If the timing metric (8) is $M(d)={\frac {|P(d)|^{2}}{(R(d))^{2}}}$, we calculate the normalization as $R(d)={\frac {1}{2}}\sum _{k=0}^{N-1}|r_{k+d}|^{2}$ (N=fft_len),

meaning that we estimate the energy from both half-symbols. This avoids spurious detects at the end of a burst, when the energy level suddenly drops.

[1] Schmidl, T.M. and Cox, D.C., "Robust frequency and timing synchronization for OFDM", Communications, IEEE Transactions on, 1997.

Parameters

(R): Run-time adjustable

FFT Length

FFT Length

Cyclic Prefix Length

Length of the guard interval (cyclic prefix) in samples

Preamble Carriers

If true, the carriers in the sync preamble are occupied such that the even carriers are used (0, 2, 4, ...). If you use all carriers, that would include the DC carrier, so be careful.

Threshold (R)

detection threshold. Default is 0.9.

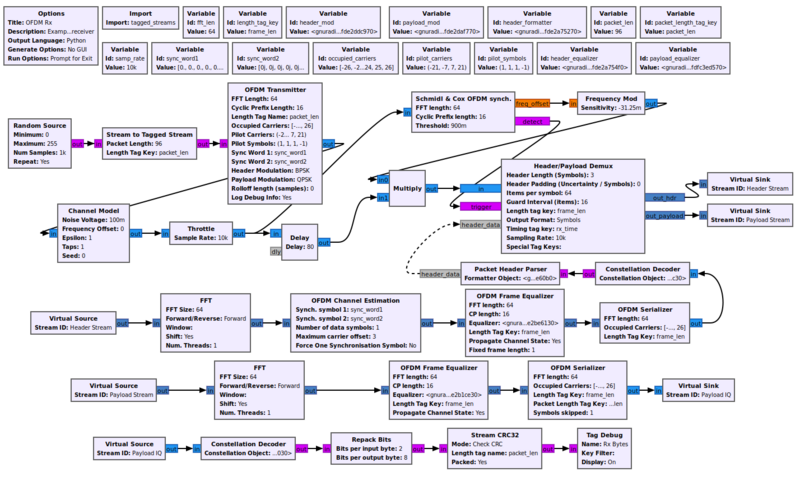
Example Flowgraph

This flowgraph can be found at [1].

Source Files

C++ files

[2]

Header files

[3]

Public header files

[4]

Block definition

[5]