QPSK Mod and Demod: Difference between revisions
| Line 79: | Line 79: | ||
=== Polyphase Clock Sync === | === Polyphase Clock Sync === | ||
The Polyphase Clock Sync provides three functions. First, it performs the clock recovery. Second, it provides the receiver matched filter to remove the ISI. Third, it down-samples the signal (reduces the samples per symbol). | |||
The example flowgraph [[Media:Qpsk_stage3.grc]] takes the output of the channel model and passes it through a Polyphase Clock Sync block. This block is setup with 32 filters and a loop bandwidth of 2pi/100. The block also takes in a value for the expected samples per symbol. | |||
[[File:Qpsk_stage3_fg.png|800px]] | |||
[[File:Qpsk_stage3_out.png|800px]] | |||
When running this script, we see the constellation is still a little noisy as a result of the ISI after the 32 filters, but is quickly absorbed by noise once we adjust the channel Noise Voltage setting to be more than 0. | |||
=== Multipath === | === Multipath === | ||
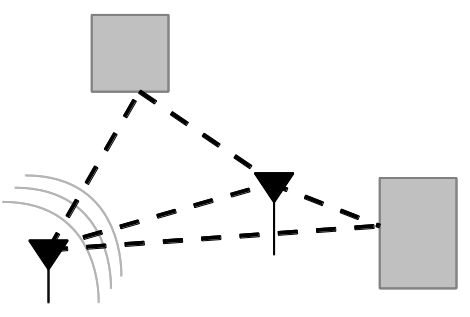
Multipath results from that fact that in most communication environments, we don't have a single path for the signal to travel from the transmitter to the receiver. Like the drawing below shows, any time there is an object that is reflective to the signal, a new path can be established between the two nodes. Surfaces like buildings, signs, trees, people, etc. can all produce signal reflections. Each of these reflective paths will show up at the receiver at different times based on the length of the path. Summing these together at the receiver causes distortions, both constructively and destructively. | |||
[[File:Multipath_cartoon.png|Multipath drawing]] | |||
=== Equalizer === | === Equalizer === | ||
Revision as of 03:29, 3 December 2023
NOTICE! This is a work in progress, but ultimately will replace Guided Tutorial PSK Demodulation.
Introduction
Objectives
- Understand issues of signal distortion and channel effects.
- Recognize the stages required to transmit and receive QPSK signals.
Prerequisites
The student should study each of the sections under the "Flowgraph Fundamentals" heading in Tutorials before attempting to do this tutorial.
References
- The ARRL Handbook, "Quadrature Modulation" section (any recent edition)
- f. j. harris and M. Rice, "Multirate Digital Filters for Symbol Timing Synchronization in Software Defined Radios", IEEE Selected Areas in Communications, Vol. 19, No. 12, Dec., 2001. [1]
- J. Feigin, "Practical Costas loop design: Designing a simple and inexpensive BPSK Costas loop carrier recovery circuit," RF signal processing, pp. 20-36, 2002
- Our Suggested Reading list
Notes
This tutorial has been revised and tested with GNU Radio version 3.10.8.0. It strives to provide consistent flowgraphs where each stage builds on the previous one, maintaining the same parameters from one stage to the next.
It is intended that the reader study the flowgraphs and resulting output, but not necessarily build each one. However, links to GRC source files are included.
Transmitting a QPSK Signal
The first stage is transmitting the QPSK signal. We generate a stream of bits and modulate it onto a complex constellation. To do this, we use the Constellation Modulator block, which uses a Constellation Rect. Object and other settings to control the transmitted signal. The Constellation parameter of the Constellation Modulator is the id of the Constellation Rect. Object (qpsk), even though it shows on the flowgraph as something else.
The constellation object specifies how the symbols are coded. The modulator block can then use this modulation scheme with or without differential encoding. The constellation modulator expects packed bytes, so we have a random source generator providing bytes with values of 0 to 255.
When dealing with the number of samples per symbol, we want to keep this value as small as possible (minimum value of 2). Generally, we can use this value to help us match the desired bit rate with the sample rate of a hardware device. But since we're using simulation, the samples per symbol is only important in making sure we match this rate throughout the flowgraph. We'll use 4 here, which is greater than what we need, but useful to visualize the signal in the different domains.
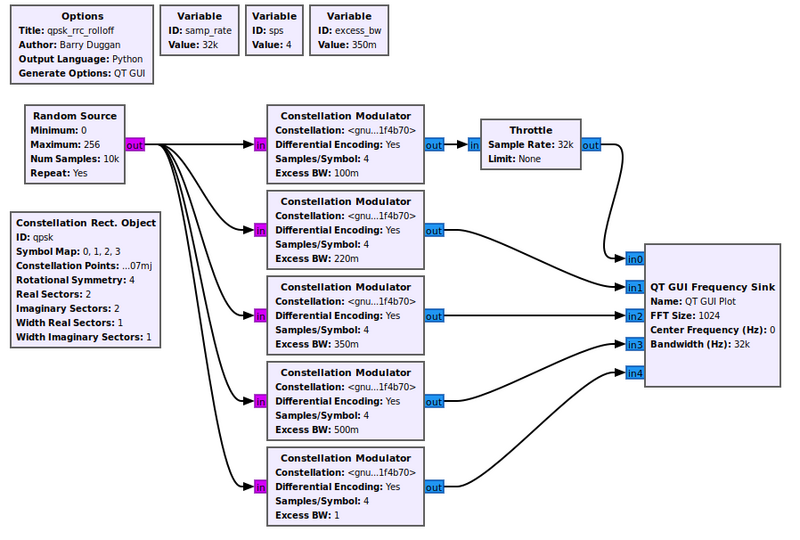
Excess Bandwidth
The constellation modulator uses a root raised cosine (RRC) pulse shaping filter to control the bandwidth of the transmit signal. That parameter is called "Excess BW" (excess bandwidth).
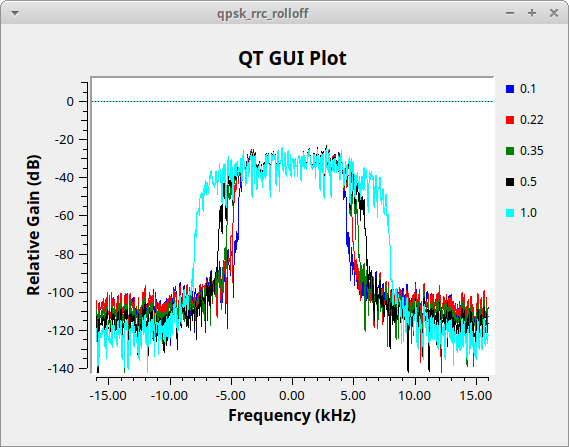
The flowgraph below, Media:Qpsk_rrc_rolloff.grc, generates the following figure showing different values of the excess bandwidth. Typical values used are between 0.2 (red trace) and 0.35 (green trace). We will use 0.35 in this tutorial.
Matched Filters and ISI
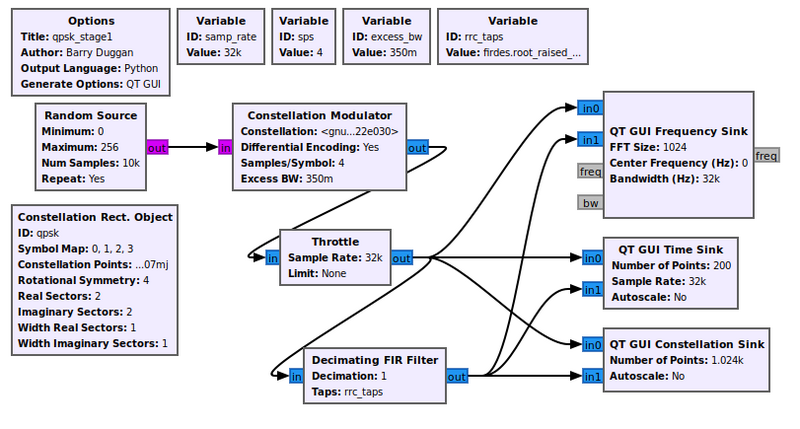
The example flowgraph, Media:Qpsk_stage1.grc, transmits a QPSK constellation. It plots both the transmitted signal and part of the receiver chain in time, frequency, and the constellation plot. The variable rrc_taps value is firdes.root_raised_cosine(1.0,samp_rate,samp_rate/sps,excess_bw,11*sps).
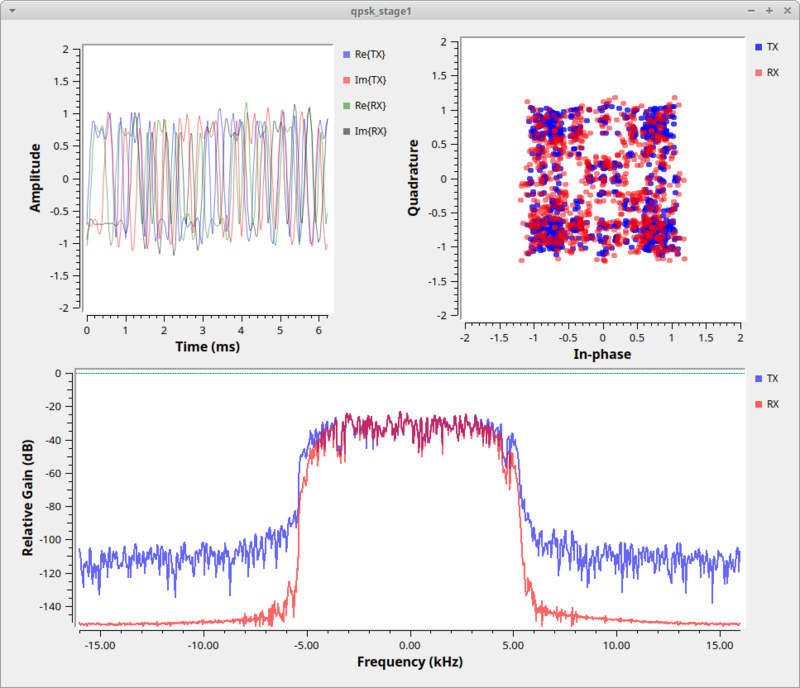
In the constellation plot below, we see the effects of the up-sampling (generating 4 samples per symbol) and filtering process. The RRC filter limits the transmit bandwidth so the signal is within our desired bandwidth. If we didn't put a shaping filter on the signal, we would be transmitting square waves which produce a lot of energy in the adjacent channels.
A side effect of the RRC filter is to create inter-symbol interference (ISI). ISI is bad for a received signal because it blurs the symbols together. We'll look into this in-depth during the timing recovery section.
On the receive side, we get rid of ISI by using another filter. Basically, what we've done is used a filter on the transmitter, the RRC filter, which creates the ISI. But when we convolve two RRC filters together, we get a raised cosine filter (which is a form of a Nyquist filter). So, knowing this property of the transmit RRC filter, we can use another RRC filter at the receiver to minimize ISI.
Channel Impairments
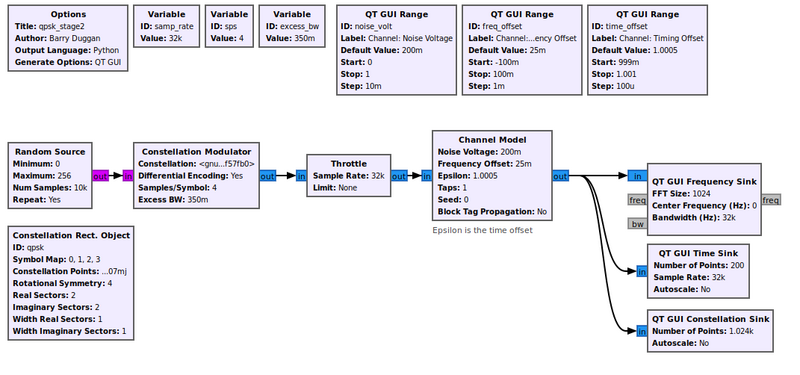
The first stage example only dealt with the mechanics of transmitting a QPSK signal. We'll now look into the effects of the channel and how the signal is distorted between when it was transmitted and when we see the signal in the receiver. The first step is to add a channel model, which is done using the example Media:Qpsk_stage2.grc below. We'll use the basic Channel Model block of GNU Radio.
This block allows us to simulate a few main issues that we have to deal with. The first issue with receivers is noise. Thermal noise in our receiver causes noise that we know of as Additive White Gaussian Noise (AWGN). We set the noise power by adjusting the noise voltage value of the channel model. We specify the voltage here instead of power because we need to know the bandwidth of the signal in order to calculate the power properly. We can calculate the noise voltage from a desired power level knowing the other parameters of the simulation.
Another significant problem between two radios is different clocks, which drive the frequency of the radios. The clocks are, for one thing, imperfect, and therefore different between radios. One radio transmits nominally at fc (say, 450 MHz), but the imperfections mean that it is really transmitting at fc + f_delta_1. Meanwhile, the other radio has a different clock and therefore a different offset, f_delta_2. When it's set to fc, the real frequency is at fc + f_delta_2. In the end, the received signal will be f_delta_1 + f_delta_2 off where we think it should be (these deltas may be positive or negative).
Related to the clock problem is the ideal sampling point. We've up-sampled our signal in the transmitter and shaped it, but when receiving it, we need to sample the signal at the original sampling point in order to maximize the signal power and minimize the inter-symbol interference. Like in our stage 1 simulation after adding the second RRC filter, we can see that among the 4 samples per symbol, one of them is at the ideal sampling point of +1, -1, or 0. But again, the two radios are running at different speeds, so the ideal sampling point is an unknown.
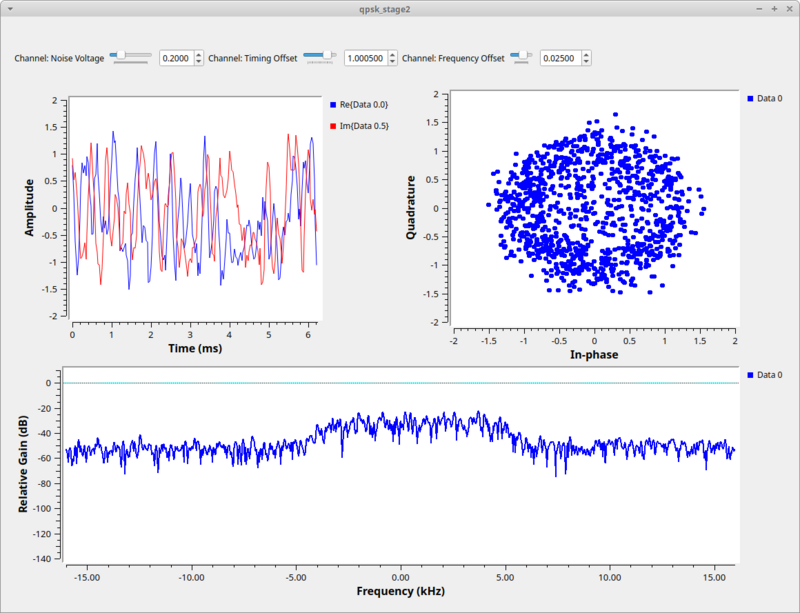
The second stage of our simulation allows us to play with these effects of additive noise, frequency offset, and timing offset. When we run this graph we have added a bit of noise (0.2), some frequency offset 0.025), and some timing offset (1.0005) to see the resulting signal.
The constellation plot shows us a cloud of samples, far worse that what we started off with in the last stage. From this received signal, we now have to undo all of these effects.
Receiving a QPSK signal
Polyphase Clock Sync
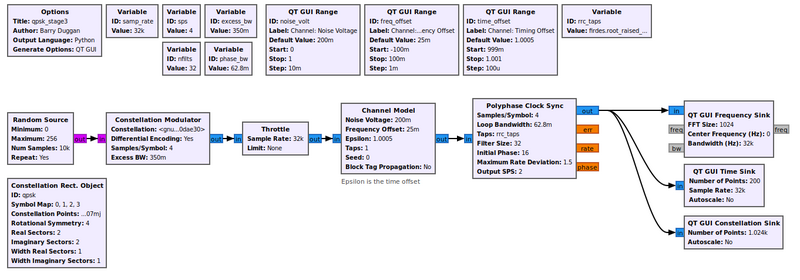
The Polyphase Clock Sync provides three functions. First, it performs the clock recovery. Second, it provides the receiver matched filter to remove the ISI. Third, it down-samples the signal (reduces the samples per symbol).
The example flowgraph Media:Qpsk_stage3.grc takes the output of the channel model and passes it through a Polyphase Clock Sync block. This block is setup with 32 filters and a loop bandwidth of 2pi/100. The block also takes in a value for the expected samples per symbol.
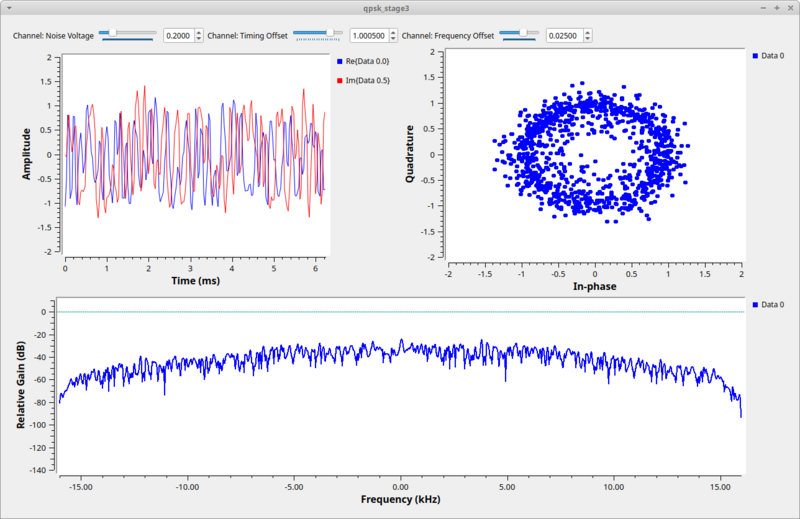
When running this script, we see the constellation is still a little noisy as a result of the ISI after the 32 filters, but is quickly absorbed by noise once we adjust the channel Noise Voltage setting to be more than 0.
Multipath
Multipath results from that fact that in most communication environments, we don't have a single path for the signal to travel from the transmitter to the receiver. Like the drawing below shows, any time there is an object that is reflective to the signal, a new path can be established between the two nodes. Surfaces like buildings, signs, trees, people, etc. can all produce signal reflections. Each of these reflective paths will show up at the receiver at different times based on the length of the path. Summing these together at the receiver causes distortions, both constructively and destructively.