Gr4-packet-modem receiver
This page describes the operation of the gr4-packet-modem receiver.
The packet receiver is implemented as a class that adds and connects multiple blocks to an existing gr::Graph. This is done like so because at the moment hierarchical flowgraphs are not supported in GNU Radio 4.0.
Flowgraph
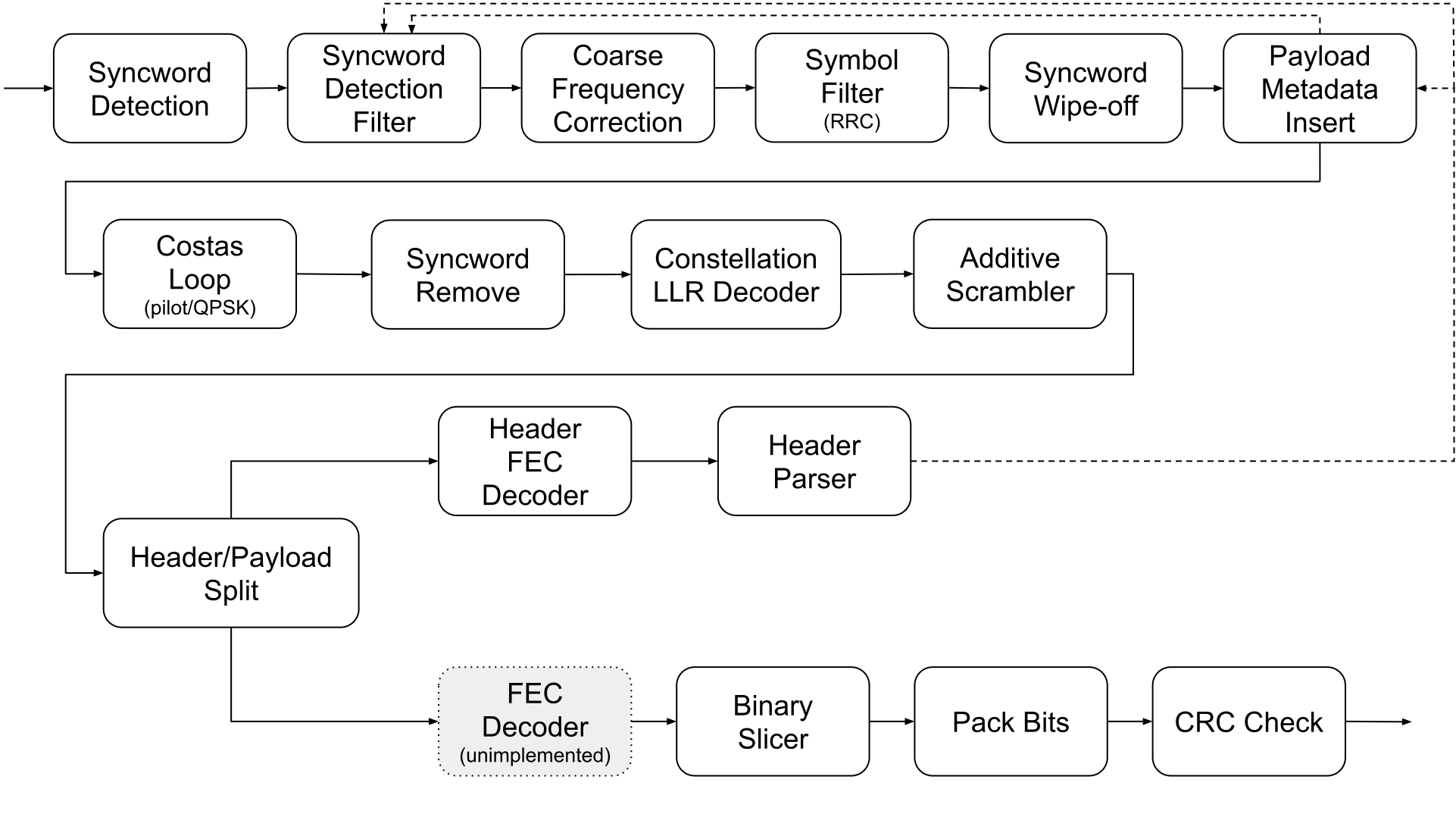
The flowgraph of the packet receiver is shown here. Blocks in grey are not present, but could be added to the flowgraph. The functionality of the flowgraph is described below. This assumes some familiarity with the packet structure defined in gr4-packet-modem waveform design.
The Syncword Detection block receives IQ samples at an integer number of samples/symbol (typically 4 samples/symbol). It uses FFTs to compute correlations with the synchronization words and detect the presence of a packet in the time-frequency domain. The mathematical details are described below. When a packet is detected, the block inserts tags that mark the sample in which the syncword begins, a fine time offset, indicating fractional sample delay, a carrier frequency estimate, a phase estimate, an amplitude estimate, and a CN0 estimate. The output of this block is the same stream of IQ samples as the input, with these tags inserted.
The Coarse Frequency Correction block is similar to a Rotator that can update its frequency using a tag. When this block sees a tag indicating the carrier frequency estimate at the beginning of a packet, it sets its rotator frequency to correct that frequency error, and resets its internal rotator phase to zero so that the phase estimate produced by Syncword Detection is still applicable to the output of this block. In this way, most of the frequency error of the packet is corrected. The Coarse Frequency Correction block maintains a constant frequency shift throughout all the packet, and it does not take into account any frequency drift or error in the frequency estimate produced by the Syncword Detection.
The output of Coarse Frequency Correction is sent to the Symbol Filter block. This block implements RRC matched filtering and decimation to one sample/symbol. This is performed by a polyphase FIR filter, similar to how Symbol Sync operates. However this block is open-loop. It does not try to measure and correct the symbol timing offset. It only uses the tags generated by Syncword Detection that indicate the start of the packet and its fractional sample delay to initialize the symbol timing at the beginning of the packet. This symbol timing is propagated at the nominal symbol rate throughout the packet, so this block does not handle any sampling frequency offset. This is fine for packet of a reasonable length. For instance, for a packet of 10000 symbols (which can carry around 2500 bytes with uncoded QPSK data) and a sampling frequency offset of 10 ppm, the accumulated symbol timing error at the end of the packet is only 0.1 symbols. This open-loop approach is simpler than the closed loop implemented by Symbol Sync, and it can be more robust under low SNR or fading conditions, as it only relies on the accuracy of the timing estimate done on the synchronization word. The Symbol Filter block also uses the amplitude estimate tags produced by Syncword Detection to normalize its output to unit amplitude (the constellation symbols are normalized to the amplitude of the reference constellation). Design note: Since most of the frequency error has been removed by Coarse Frequency Correction, the SNR losses caused by integrating symbols with the matched filter in presence of a frequency error are very small. This is the reason why the Coarse Frequency Correction block is included before Symbol Filter.
The Syncword Wipe-off block receives the one sample/symbol output of Symbol Filter and wipe off the known 64-bit pattern of the synchronization word at the beginning of each packet, so that all the IQ symbols of the synchronization word at the output are +1 (which acts as a pilot signal). This blocks knows where the synchronization word occurs in the sample stream because of the tags inserted by Syncword Detection, which have been propagated appropriately by Symbol Filter. Note that up to this point the stream of samples throwing to the blocks corresponds to all the samples in the input signal. The gaps between packets have not been discarded yet, and the lengths of the packets are not known until the header is decoded and parsed.
Payload Metadata Insert is critical for the operation of the rest of the flowgraph. It works in the following way. It first drops input samples until it sees a tag marking the beginning of a packet. Then it passes the first 64 + 128 symbols of the packet to the output. These 64 + 128 symbols correspond to the synchronization word and header. The downstream blocks will use these symbols to decode and parse the header, in order to find the packet length and potentially other properties such as its payload MODCOD (in this implementation the only MODCOD possible is uncoded QPSK, but the system is designed to allow other MODCODs). The Payload Metadata Insert now blocks waiting for a gr::Message that contains the "metadata" (packet length, packet type, etc.) decoded from the header. In this state, the block does not consume any input and does not produce any output. When the message eventually arrives, the block starts passing the payload of the packet to the output. It inserts tags at the beginning of the payload indicating what is the payload length and what is the constellation (and potentially what is the FEC type, if different FECs were supported for the payload). The block only passes to the output as many samples as there are symbols in the payload (which it knows because of the payload length in the metadata message). Once the end of the payload is reached according to this count, the block goes back to its initial state in which it drops input until it sees a tag indicating that a packet begins. In this way, the output of Payload Metadata Insert is a stream of back-to-back packets, appropriately cut from the continuous symbol stream to their correct payload length, and with some metadata tags inserted at the beginning of the payload. In order to produce this output, the block needs to first pass the header to the output, and then wait for the header to be decoded before passing the payload to the output. The block must also allow for the possibility that decoding of a header fails. In this case, a gr::Message indicating decoding failure is received instead of the usual metadata message. The block then changes immediately to the "outside packet" state, passing no payload symbols to the output.
The Costas Loop block is used for closed loop recovery of phase and frequency. This block can use phase error detectors for different constellations, and it can change the phase error detector at runtime according to tags in the input that indicate which constellation is used. The block can also set an initial phase as indicated by input tags. In this flowgraph, the Costas Loop is set to the phase estimate obtained by Syncword Detection and to a frequency of zero at the beginning of a packet. Recall that the Coarse Frequency Correction block has removed most of the frequency error, so the closed loop can lock easily under these conditions. Since the synchronization word symbols have been wiped off, the Costas Loop operates with the synchronization word as a pure pilot signal. The phase error detector for this (a 4-quadrant arctangent) does not have squaring losses, unlike a BPSK phase error detector. This is the reason why the synchronization word has been wiped off. At the beginning of the header, a tag that has been inserted by Payload Metadata Insert causes the Costas Loop to switch to a QPSK phase error detector. Then it processes the payload with a QPSK phase error detector, but if a different constellation was used, the Costas Loop could switch the phase error detector according to a tag inserted by Payload Metadata Insert. The Costas Loop uses a second order loop with the loop coefficients calculated according to the paper Controlled-Root Formulation for Digital Phase-Locked Loops. Although it is not mentioned in the paper, for the second order case it is possible to write explicit formulas for the loop coefficients in terms of the noise bandwidth. This is explained in a computing PLL coefficients blog post. The Costas Loop block uses these explicit formulas. The noise bandwidth of the loop can be updated at runtime in response to input tags. The Payload Metadata Insert block has a configuration of different bandwidths to use for the synchronization word, the header, and the payload (the bandwidth gets progressively smaller). A tag is inserted at the beginning of each of these sections to update the Costas Loop bandwidth.
Design note: Ideally, a flowgraph like this would perform frequency correction only at the point where the Coarse Frequency Correction block is placed. The Costas Loop would only run the phase error detector and loop filter, and then feed back information to the upstream frequency correction block. In this way, the frequency error that Symbol Filter sees when the loop has converged is zero. This feedback loop that encompasses multiple blocks requires a loop in the flowgraph. These are allowed by GNU Radio 4.0. However, flowgraphs loops are still not easily applicable to this situation. GNU Radio blocks often work with chunks of thousands of samples at a time for performance reasons. Because of this, a flowgraph loop would introduce a delay of thousands of samples in the loop update, which interferes with the correct operation of the loop. The solution would be to force all the blocks that form part of the loop to process only very few samples at a time, so as to reduce the delay of the loop update. This would perhaps cause CPU performance problems.
After the Costas Loop, the Syncword Remove drops the first 64 symbols of each packet in order to remove the synchronization word, which is not needed anymore. Design note: the reason for preserving the synchronization word until this point and in particular running it through the Costas Loop is to take advantage of the presence of the syncword to make the loop converge during the syncword, before the header begins, even if there is a small error in the phase and frequency estimates produced by Syncword Detection.
The Constellation LLR Decoder block now processes the symbol stream to convert complex symbols into log-likelihood ratios for each bit. As is common in the literature, this block uses the convention that a positive LLR represents that the bit 0 is more likely. Similarly to the Costas Loop, the Constellation LLR Decoder can change the constellation that it uses at runtime according to input tags. However, in this flowgraph it is only used with the QPSK constellation. Note that a constellation change can imply a change in the resampling ratio of the block (the block converts one complex symbol into bits/symbol float LLRs). At the moment this runtime change of the resampling ratio is possible but slightly problematic with the GNU Radio 4.0 runtime (the processBulk() call in which the change has just happened still uses the old resampling parameters to determine the sizes of the input and output spans).
The Additive Scrambler block performs descrambling of the header and payload by inverting the sign of the LLRs when needed. The state of the scrambler is reset at the beginning of each header according to a tag inserted by the Payload Metadata Insert block.
The Header/Payload Split block is also important for the operation of the receiver. It splits the header and payload sections of the packet, sending each to one output. The block knows the length of the header, and it uses input tags inserted by Payload Metadata Insert to determine the length of the payload. It also needs to account for the possibility that the header decoding has failed. In this case the Payload Metadata Insert has not produced any payload output, so the tag indicating the payload length is not present immediately after the end of the header. When this happens, Header/Payload Split deduces that the header decode has failed and so no payload has been produced, and it passes directly to processing the next header.
The header LLRs go into the Header FEC Decoder block. This block first processes the r=1/2 repetition coding by adding the LLRs of each pair of repeated bits. Then it runs an LDPC decoder to decode the (128, 32) LDPC codeword. The C API bindings of the ldpc-toolbox Rust library are used for this. The LDPC decoder algorithm used is know as HLAminstari8. This consists of horizontal layered message passing scheduling, an Approximate-MIN* rule for belief propagation, and int8_t arithmetic for the LLRs. The decoder runs until a valid LDPC codeword is obtained or the maximum of 25 iterations is reached. If a valid LDPC codeword is not obtained, the decoder inserts a tag indicating that the header is invalid, but still passes the decoded bits to the output. The output of this block is packed as 8 hard bits per byte.
The Header Parser block receives the decoded headers. It parses the header fields and extracts information into a gr::Message, which is sent to Payload Metadata Insert. The Header Parser can declare header decoding failure, either if the Header FEC Decoder block has already declared an LDPC decoder failure, or if some of the header fields have invalid values. In this case, a message indicating the decoding failure is sent to Payload Metadata Insert instead of the regular message.
The flowgraph architecture has the provision for a Payload FEC Decoder, which receives the payload LLRs from Header/Payload Split and performs FEC decoding. This block could select the FEC algorithm to use according to tags inserted by Payload Metadata/Insert. Currently this block is not implemented, because the payload has no FEC.
The payload LLRs (potentially after FEC decoding) are sent to a Binary Slicer block that converts them to hard bits. Unlike the GNU Radio 3.10 Binary Slicer, this block supports the convention that a positive LLR corresponds to the bit 0 (it also supports the opposite convention). The hard bits are packed as 8 bits/byte by a Pack Bits block. Then a CRC Check computes and checks the CRC-32 of the payload and discards the packet if the CRC is not correct. Packets with a correct CRC-32 are sent to the output of the receiver. Due to how tag propagation works, all the header information is available as tags at the beginning of the packet.
Syncword detection
The Syncword Detection block uses correlation with the RRC filtered and modulated synchronization word to detect the presence of a packet in the time-frequency domain. The correlation can be understood as a matched FIR filter using the complex conjugate of the modulated synchronization word as taps (since the synchronization word is BPSK modulated, it is actually a real signal). The FIR filter is implemented using FFTs with the overlap-save method.
At initialization, the Syncword Detection block uses the supplied syncword, constellation, rrc_taps, and samples_per_symbol parameters to compute the modulated syncword at complex baseband. The length of the modulated syncword is syncword_size = (syncword.size() - 1) * samples_per_symbol + rrc_taps.size().
To perform the search in the frequency domain, the Syncword Detection block takes min_freq_bin and max_freq_bin parameters. These refer to the indices of the frequency bins to cover in the search (both the min_freq_bin and the max_freq_bin are included in the search). The separation of the frequency bins is equal to 0.5 * samp_rate / syncword_size (Design note: the frequency response of the matched filter roughly looks like a sinc function with zeros at multiples of samp_rate / syncword_size. Therefore, half of this value is chosen as bin separation to minimize the correlation losses). Index 0 corresponds to baseband. For each of the indices included in the frequency search range, the modulated syncword is shifted to that particular frequency, thus obtaining a filterbank of max_freq_bin - min_freq_bin + 1 filters.
The Syncword Detection block also takes an fft_size parameter. For good CPU performance this should be several times larger than the length of the modulated syncword, in order to reduce the overhead of the overlap-save method. By default, an FFT size of 2048 points is used, which is adequate for a syncword of 64 symbols, 4 samples per symbol, and a length of 45 for the RRC taps (these parameters give a modulated syncword_size = 297). The complex conjugate of the FFT (using this number points) of each of the modulated syncwords at different bins is pre-computed in the initialization.
The Syncword Detection works by reading blocks of fft_size input samples, but only stepping by stride = fft_size - syncword_size + 1 samples, so as to implement the overlap-save method. The FFT of each block is computed and multiplied by the pre-computed conjugate FFTs of each of the modulated syncwords at different frequency frequency bins. For each block, an estimate of the noise floor is obtained by averaging the outermost 1/2 of the FFT bins of the FFT of the signal (this is 1/4 of bins on the left edge and 1/4 of the bins on the right edge of the spectrum). Since the signal is RRC filtered at 4 samples/symbol, this part of the spectrum should only contain noise. The noise floor estimate is only used to estimate the CN0.
For each block, there are stride samples that are valid outputs of the overlap-save method. These represent different delays. For each of these delay, the frequency bin where the correlation (matched filter) power is largest is found. The parameters corresponding to that correlation are saved by pushing them to the end of a buffer (implemented using HistoryBuffer). These parameters include the complex value of the correlation, its power, the power of the two adjacent frequency bins, the frequency bin index, the corresponding input IQ sample, and the noise floor estimate.
A local maximum search algorithm runs on the elements of this buffer to detect the correlation peak that would correspond to the presence of a syncword in the input signal. The algorithm keeps track of whether the correlation power obtained in the previous step is the best so far or not, thus keeping track of the local maximum candidate. Once the local maximum candidate is "old enough", it is declared as a local maximum and a check is done to determine if the maximum is above the detection threshold. This "old enough" condition is imposed to ensure that the syncword detection triggers with the actual correlation peak produced by the syncword, and not with a smaller correlation peak near it (for instance caused by auto-correlation sidelobes of the syncword). Therefore, this procedure establishes a window of length time_threshold samples. To be declared as a local maximum, the peak must be larger than all the other values within ±time_threshold samples. The time_threshold is determined to be somewhat shorter than the length of the modulated syncword and header, since it is impossible to find two syncwords that are separated by less than this distance.
The detection threshold is checked in the following manner. The criteria is that the correlation peak should be larger than a certain power_threshold times the median of the correlation power values in the HistoryBuffer. In order to check this condition without computing the median itself (which involves sorting the values), the algorithm counts how many such values are below the power of the correlation peak divided by power_threshold. The criteria involving the median is equivalent to the fact that more than half of the elements in the buffer are below that threshold. If the detection criteria is satisfied, the correlation peak element in the buffer is marked as a valid detection.
The size of the buffer is kept fixed to history_size = 2 * time_threshold + 1 elements. For every element that is pushed to the buffer, another element is popped from the other end. The input IQ sample value in this element is passed to the output of Syncword Detection, so the Syncword Detection block introduces a delay of history_size in its output (the first history_size output samples produced are zero, and the following output samples coincide with the input samples). This is done because an output sample cannot be produced until it is known whether the sample should carry tags marking a detection or not, and evaluating this requires looking ahead at some samples "in the future" to implement the local maximum condition, so a delay needs to be introduced in the output (to make the block "causal").
When an element is popped from the buffer to produce an IQ output sample, the detection flag in this element is checked (at this point it has already been evaluated whether this element constitutes a successful detection). The remaining values in the element are used to produce the metadata that accompanies the detection. Quadratic interpolation using the power of the correlation peak and the two adjacent frequency bins is done to obtain a frequency estimate that has sub-frequency-bin resolution. The phase is computed from the phase of the complex correlation. An amplitude estimate is derived from the amplitude of the correlation. An Es/N0 estimate is computed using the amplitude estimate and the noise floor estimate. A quadratic interpolation involving the correlation power and the correlation power of the previous and next element in the buffer is done to estimate a fine sub-sample delay. All of these estimates are inserted as tags in the output IQ sample.