Rotator
The Rotator block performs a frequency translation. This operation is called a rotation because if you plot the real and imaginary numbers in a complex sample (I and Q) in a complex unit circle, rotating around this circle produces a wave at a given frequency. Making such a rotation clockwise or counterclockwise produces a positive or negative frequency, which is effectively what this block does mathematically.
Mathematical Description
The phase increment (in radians) is the amount of additional phase shift added to the signal every sample. So, the block is the equivalent of multiplying by a complex sine.
Remember that a complex sine of frequency is a signal composed of exactly one element in the frequency domain. Looking at its complex argument, i.e., the angle of it at any time in the complex plane, it's simply .
We're working with sampled signals, so we only observe it every sample interval . Between two sample instants, the phase grows by ; thus, to achieve a specific frequency shift , one has to calculate the phase increment from the desired frequency.
Parameters
(R): Run-time adjustable
- Phase Increment (R)
- Acts as the rotational velocity.
Example Flowgraph
Example 1
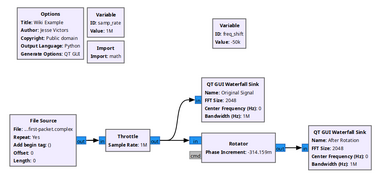
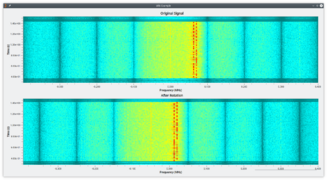
In the example below, the Rotator block shifts a stream of samples down 50 kHz. In this example, a Frequency-Shift Keying signal is captured slightly offset because the HackRF One generates a large spike at the exact center frequency. The solution is to simply capture at an offset and then use the Rotator to re-adjust the frequency alignment as desired.
Example 2
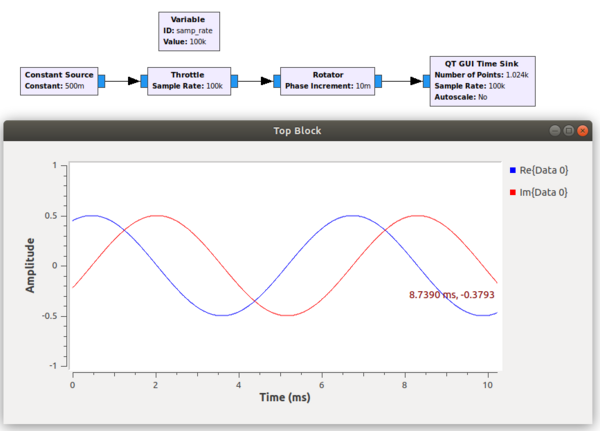
In the example below a constant source, set to 0.5, is fed into the rotator, thus producing a sine wave. The phase increment is set to 0.01 radians and the sample rate is 100kHz, so that equates to 1000 radians every second, or 1000/(2pi) = 159 cycles per second. This corresponds to a period of about 6ms, as shown in the time sink.
Source Files
- C++ files
- TODO
- Header files
- TODO
- Public header files
- TODO
- Block definition
- TODO