Quadrature Demod
The Quadrature Demod block performs frequency demodulation. It accepts a stream of complex samples, such as the narrow baseband stream containing the desired signal, and produces a stream of floats that are the frequency demodulated output of the original signal. This block is most useful in demodulating FM, FSK, GMSK, and similar modulations that carry information through changes in frequency.
This block does not support C++ output, so it cannot be used when the output language of a flowgraph in GRC is C++.
General Description
Frequency modulation, as the name implies, changes the frequency of the carrier in concert with the input information. Frequency is a change of phase over time. (In math terms, frequency is the differential of phase.) In order to frequency demodulate a carrier, it's necessary to calculate the phase change between consecutive samples. The image below shows how two samples from an FM signal might appear on an Argand diagram. This signal can be frequency demodulated by calculating the phase difference between these consecutive samples.
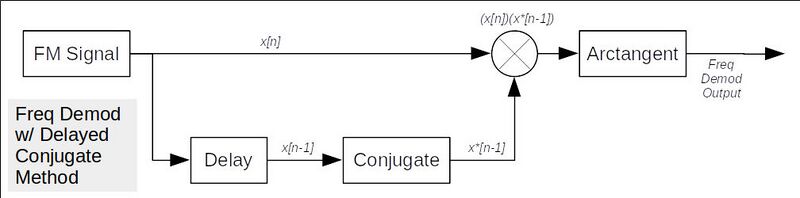
The most straightforward method to calculate the phase change is to multiply each complex sample with a conjugated version of the sample that came before it. A block diagram of this would appear as follows:
This is a polar discriminator circuit. A Gnu Radio block diagram equivalent to the Quadrature Demod block would be as follows:
This GRC flowgraph is the equivalent of the Quadrature Demod block, as described above. The Multiply Const block provides the equivalent of the "Gain" value in the Quadrature Demod block. The output of the Complex to Arg block is a set of real samples. Each sample is the phase difference, in radians, from the value before it. To change this from radians to cycles, these values must be divided by 2 π. To convert this to frequency, these values must be divided by the sample period. Dividing by the sample period is equivalent to multiplying by the sample rate. Hence, the default "Gain" value should be:
where is the sample rate. The units of the output of this would be hertz (Hz). To normalize this, the values can also be divided by the deviation of the signal. This would provide a gain value of:
where "deviation" is the deviation, in Hz, of the signal being demodulated. By default, the variable name for this deviation value in the Quadrature Demod block is "fsk_deviation_hz", but this variable can be changed to any name desired, and it does not mean that the input signal must be FSK (it can be analog FM, for example).
Mathematical Description
The output of the block is the signal frequency in relation to the sample rate, multiplied with the gain. It produces this by calculating the product of the one-sample delayed-&-conjugated input and the undelayed signal, and then calculates the argument (a.k.a. angle, in radians) of the resulting complex number:
Let x be a complex sinusoid with amplitude A>0, (absolute) frequency and phase sampled at f_s>0 so, without loss of generality,
then
is real, and so is , and hence only scales, therefore is invariant: = arg
Parameters
- Gain
- Gain setting to adjust the output amplitude. Set based on converting the phase difference between samples to a nominal output value. Default: "samp_rate/(2*math.pi*fsk_deviation_hz)".
Example Flowgraph
Example 1: Analog FM Signal
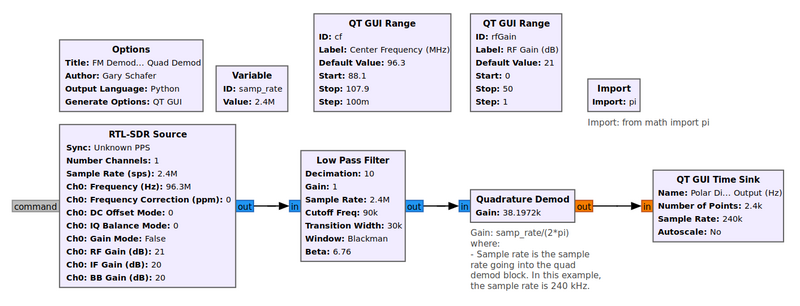
An example flowgraph of this block for an analog FM station is shown below.
The output of a SDR (a RTL-SDR, in this example) is sent to a FFT Low Pass Filter, where the only signal that passes through is the analog FM signal. The output is sent to the Quadrature Demod block, where it is frequency demodulated. The "Gain" setting for this block is samp_rate/(2*pi). To normalize this output, meaning to make the maximum limits +/- 1, this equation can be changed to samp_rate/(2*pi*deviation), where deviation is the actual deviation of the transmitter, in Hz.
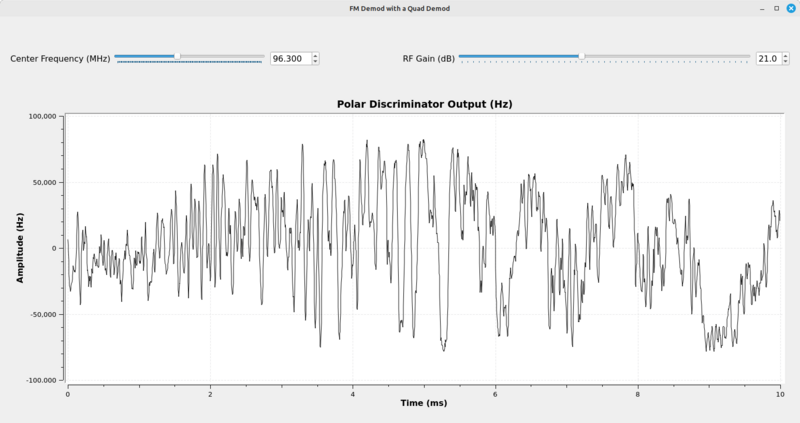
The output of this flowgraph appears as follows:
The amplitude limits of the QT GUI Time Sink are +/- 100 kHz (100e3). By pausing the signal, it's possible to measure the maximum deviation of the station.
Example 2: FSK Signal
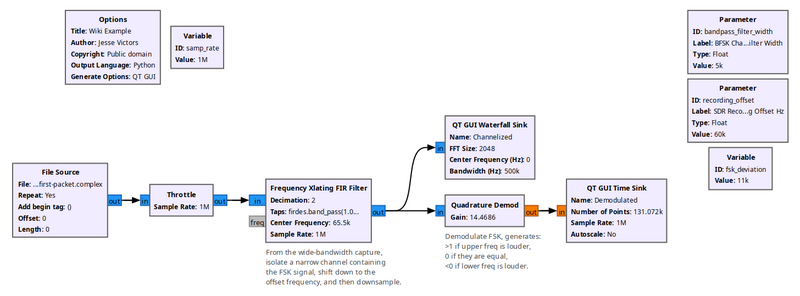
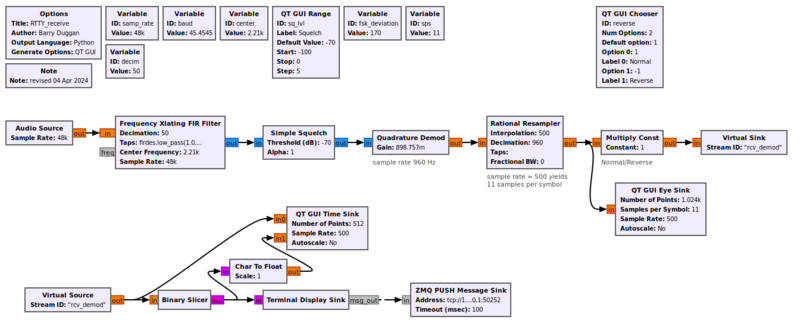
An example flowgraph of this block, demonstrating the demodulation of a narrow FSK signal inside a wideband capture file.
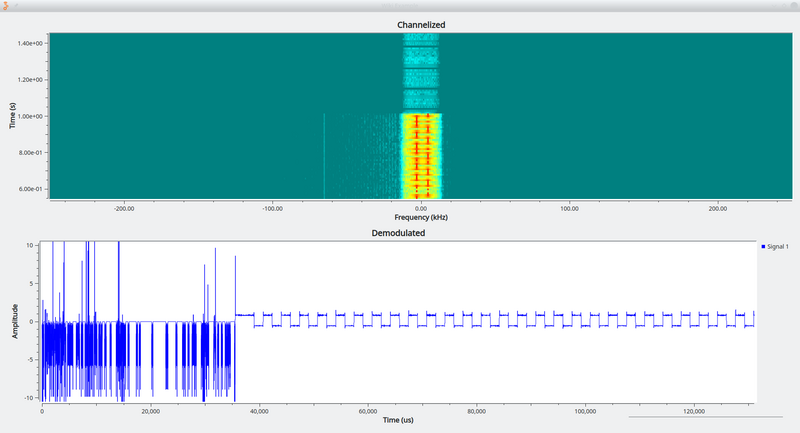
The Quadrature Demod block in practice extracts the symbols from the FSK signal. Random noise is produced before and after the signal.
This flowgraph shows the Quadrature Demod block as a Frequency Shift Keying detector. First, the Frequency Xlating FIR Filter acts as a channelizer, extracting a narrow baseband signal from a wider stream. Then the Quadrature Demod block returns floats that are >1 if the upper frequency is louder, 0 if they are equal, and <0 if the lower frequency is louder, thus demodulating FSK. In this scenario, if fsk_deviation is defined as the difference between the upper and lower frequencies, and the baseband sampling rate is known (after the decimating from the Freq Xlating FIR Filter block), then a good formula for the Gain parameter would be baseband_samp_rate / (math.pi * fsk_deviation). This causes the block to produce output floats that will never have a magnitude greater than 1.0 for the actual symbols.
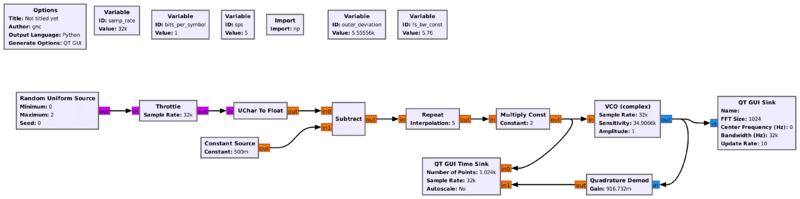
Example 3: BFSK (2FSK) Signal
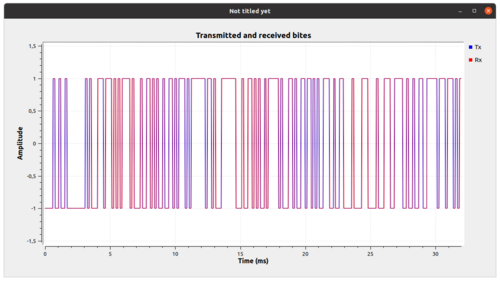
This flowgraph shows BFSK signal recovery using Quadrature Demod block
Transmitted and received bits using above example
Source Files
- C++ files
- quadrature_demod_cf_impl.cc
- Header files
- quadrature_demod_cf_impl.h
- Public header files
- quadrature_demod_cf.h
- Block definition
- analog_quadrature_demod_cf.block.yml





![{\displaystyle y[n]=\mathrm {arg} \left(x[n]\,{\bar {x}}[n-1]\right)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/84c630130d2bec382313f6da607e7df434cc7613)

![{\displaystyle \phi _{0}\in [0;2\pi ]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/83317d39f55e8bd895248ce082aa5b5dac28adb5)
![{\displaystyle x[n]=Ae^{j2\pi ({\frac {f}{f_{s}}}n+\phi _{0})}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7480ee4b1d7e60697cc5c58bd0e033bcb0be868b)
![{\displaystyle y[n]=\mathrm {arg} \left(Ae^{j2\pi \left({\frac {f}{f_{s}}}n+\phi _{0}\right)}{\overline {Ae^{j2\pi ({\frac {f}{f_{s}}}(n-1)+\phi _{0})}}}\right)\ }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2832f97c99af7f007a0e341db9a884aa61ad9594)