User talk:Duggabe: Difference between revisions
Tverrbjelke (talk | contribs) (→Cheers and Salutes: new section) |
No edit summary |
||
| Line 1: | Line 1: | ||
== | === Details of the Polyphase Clock Sync Block === | ||
There are various algorithms that we can use to recover the clock at the receiver, and almost all of them involve some kind of feedback control loop. Those that don't are generally data aided using a known word like a preamble. We'll use a [[Polyphase_Clock_Sync|polyphase filterbank]] clock recovery technique that can be found in ''Multirate Signal Processing for Communications Systems'' by fred harris [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.127.1757]. This block does three things for us. First, it performs the clock recovery. Second, it does the receiver matched filter to remove the ISI problem. Third, it down-samples the signal and produces samples at 1 sps. | |||
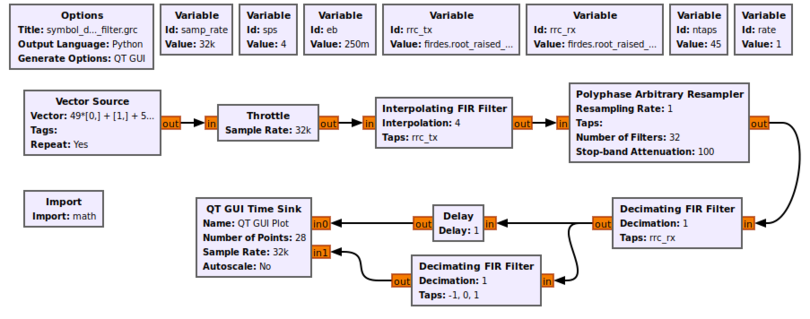
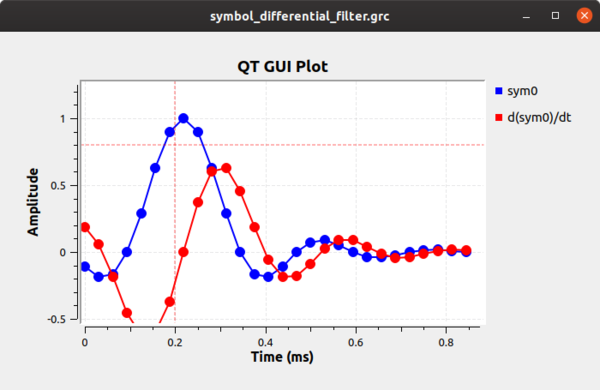
The block works by calculating the first differential of the incoming signal, which will be related to its clock offset. If we simulate this very simply at first, we can see how the differential filter will work for us. First, using the example flowgraph [https://raw.githubusercontent.com/gnuradio/gr-tutorial/master/examples/tutorial7/symbol_differential_filter.grc symbol_differential_filter.grc], we can see how everything looks perfect when our rate parameter is 1 (i.e., there is no clock offset). The sample we want is obviously at 0.22 ms. The difference filter ([-1, 0, 1]) generates the differential of the symbol, and as the following figure shows, the output of this filter at the correct sampling point is 0. We can then invert that statement and instead say when the output of the differential filter is 0 we have found the optimal sampling point. | |||
[[File:Symbol_differential_filter_grc.png|810px]] | |||
[[File:symbol_differential_filter0.png|600px]] | |||
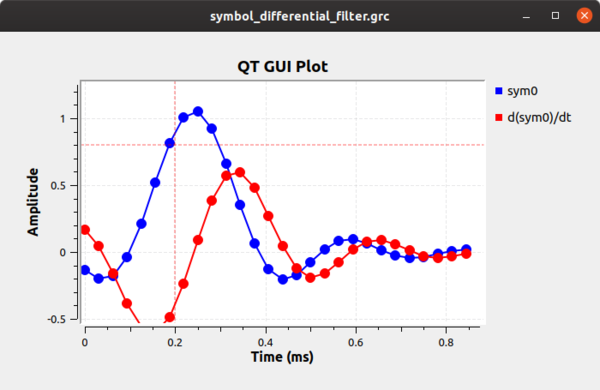
What happens when we have a timing offset? That output is shown below shows that the timing offset where the peak of the symbol is off and the derivative filter does not show us a point at zero. | |||
[[File:symbol_differential_filter1.png|600px]] | |||
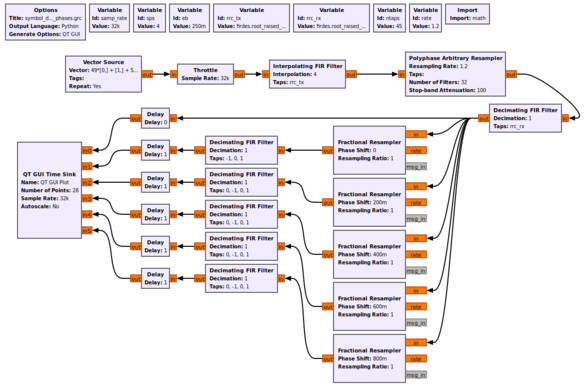
Instead of using a single filter, what we can do is build up a series of filters, each with a different phase. If we have enough filters at different phases, one of them is the correct filter phase that will give us the timing value we desire. Let's look at a simulation that builds 5 filters, which means 5 different phases. Think of each filter as segmenting the unit circle (0 to 2pi) into 5 equal slices. Using the example flowgraph [https://raw.githubusercontent.com/gnuradio/gr-tutorial/master/examples/tutorial7/symbol_differential_filter_phases.grc symbol_differential_filter_phases.grc], we can see how this helps us. Notice here that we are using the [[Fractional_Resampler|fractional resampler]] here because it makes it easy to do the phase shift (between 0 and 1), but it also changes the filter delays of the signals, so we correct for that using the follow-on delay blocks. | |||
[[File:Symbol_differential_filter_phases_grc.png|588px]] | |||
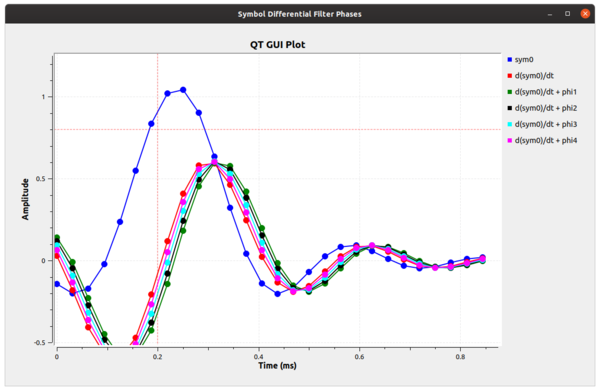
The figure below now gives us an idea of what we're dealing with, although it's a bit inexact. What we can see is that the signal labeled as d(sym0)/dt + phi3 has a sample point at 0. This tells us that our ideal sampling point occurs at this phase offset. Therefore, if we take the RRC filter of our receiver and adjust its phase by phi3 (which is 3*2pi/5), then we can correct for the timing mismatch and select the ideal sampling point at this sample time. | |||
[[File:symbol_differential_filter2.png|600px]] | |||
But as we have discussed, this is only a simulated approximation; in reality, the samples of each filter wouldn't occur at the same point in time. We have to up-sample by the number of filter (e.g., 5) to really see this behavior. However, that can clue us into what's happening a bit farther. We can look at these different filters as parts of one big filter that is over-sampled by M, where M=5 in our simple example here. We could up-sample our incoming signal by this much and select the point in time where we get the 0 output of the difference filter. The trouble with that is we are talking about a large amount of added computational complexity, since that is proportional to our sample rate. Instead, we're working on filters of different phases at the incoming sample rate, but with the bank of them at these different phases, we can get the effect of working with the over-sampled filter without the added computational cost. | |||
So in our example above, we offset our sampling rate by some known factor of 1.2 and found that we could use one of five filters as the ideal sampling point. Unfortunately, we really only have 5 different phases we can exactly produce and correct for here. Any sampling offset between these phases will still produce a mistimed sample with added ISI as we explored previously. So instead, we use way more than 5 filters in our clock recovery algorithm. Without exploring the math (see harris' book referenced above), we can use 32 filters to give us a maximum ISI noise factor that is less than the quantization noise of a 16 bit value. If we want more than 16 bits of precision, we can use more filters. | |||
So what? We have a large bank of filters where one of them is at (or very close to) the ideal sampling phase offset. How do we automatically find that? Well, we use a [http://www.trondeau.com/blog/2011/8/13/control-loop-gain-values.html 2nd order control loop], like we almost always do in these recovery situations. The error signal for the recovery is the output of the differential filter. The control loop starts at one of the filters and calculates the output as the error signal. It then moves its way up or down the bank of filters proportionally to the error signal, and so we're trying to find where that error signal is closest to 0. This is our optimal filter for the sampling point. And because we expect the transmit and receive clocks to drift relative to each other, we use a second order control loop to acquire both the correct filter phase as well as the rate difference between the two clocks. | |||
Revision as of 15:13, 16 December 2023
Details of the Polyphase Clock Sync Block
There are various algorithms that we can use to recover the clock at the receiver, and almost all of them involve some kind of feedback control loop. Those that don't are generally data aided using a known word like a preamble. We'll use a polyphase filterbank clock recovery technique that can be found in Multirate Signal Processing for Communications Systems by fred harris [1]. This block does three things for us. First, it performs the clock recovery. Second, it does the receiver matched filter to remove the ISI problem. Third, it down-samples the signal and produces samples at 1 sps.
The block works by calculating the first differential of the incoming signal, which will be related to its clock offset. If we simulate this very simply at first, we can see how the differential filter will work for us. First, using the example flowgraph symbol_differential_filter.grc, we can see how everything looks perfect when our rate parameter is 1 (i.e., there is no clock offset). The sample we want is obviously at 0.22 ms. The difference filter ([-1, 0, 1]) generates the differential of the symbol, and as the following figure shows, the output of this filter at the correct sampling point is 0. We can then invert that statement and instead say when the output of the differential filter is 0 we have found the optimal sampling point.
What happens when we have a timing offset? That output is shown below shows that the timing offset where the peak of the symbol is off and the derivative filter does not show us a point at zero.
Instead of using a single filter, what we can do is build up a series of filters, each with a different phase. If we have enough filters at different phases, one of them is the correct filter phase that will give us the timing value we desire. Let's look at a simulation that builds 5 filters, which means 5 different phases. Think of each filter as segmenting the unit circle (0 to 2pi) into 5 equal slices. Using the example flowgraph symbol_differential_filter_phases.grc, we can see how this helps us. Notice here that we are using the fractional resampler here because it makes it easy to do the phase shift (between 0 and 1), but it also changes the filter delays of the signals, so we correct for that using the follow-on delay blocks.
The figure below now gives us an idea of what we're dealing with, although it's a bit inexact. What we can see is that the signal labeled as d(sym0)/dt + phi3 has a sample point at 0. This tells us that our ideal sampling point occurs at this phase offset. Therefore, if we take the RRC filter of our receiver and adjust its phase by phi3 (which is 3*2pi/5), then we can correct for the timing mismatch and select the ideal sampling point at this sample time.
But as we have discussed, this is only a simulated approximation; in reality, the samples of each filter wouldn't occur at the same point in time. We have to up-sample by the number of filter (e.g., 5) to really see this behavior. However, that can clue us into what's happening a bit farther. We can look at these different filters as parts of one big filter that is over-sampled by M, where M=5 in our simple example here. We could up-sample our incoming signal by this much and select the point in time where we get the 0 output of the difference filter. The trouble with that is we are talking about a large amount of added computational complexity, since that is proportional to our sample rate. Instead, we're working on filters of different phases at the incoming sample rate, but with the bank of them at these different phases, we can get the effect of working with the over-sampled filter without the added computational cost.
So in our example above, we offset our sampling rate by some known factor of 1.2 and found that we could use one of five filters as the ideal sampling point. Unfortunately, we really only have 5 different phases we can exactly produce and correct for here. Any sampling offset between these phases will still produce a mistimed sample with added ISI as we explored previously. So instead, we use way more than 5 filters in our clock recovery algorithm. Without exploring the math (see harris' book referenced above), we can use 32 filters to give us a maximum ISI noise factor that is less than the quantization noise of a 16 bit value. If we want more than 16 bits of precision, we can use more filters.
So what? We have a large bank of filters where one of them is at (or very close to) the ideal sampling phase offset. How do we automatically find that? Well, we use a 2nd order control loop, like we almost always do in these recovery situations. The error signal for the recovery is the output of the differential filter. The control loop starts at one of the filters and calculates the output as the error signal. It then moves its way up or down the bank of filters proportionally to the error signal, and so we're trying to find where that error signal is closest to 0. This is our optimal filter for the sampling point. And because we expect the transmit and receive clocks to drift relative to each other, we use a second order control loop to acquire both the correct filter phase as well as the rate difference between the two clocks.