Root Raised Cosine Filter

The Root Raised Cosine Filter blocks acts as a matched filter. Its primarily purpose is extracting a known digital signal out of noise; it does this more effectively than a low-pass filter, squelch, or other blocks.

Root Raised Cosine Filter implements match filtering to pull square pulses out of an channel containing artificial Gaussian white noise.

This filter is a convenience wrapper for a FIR filter and a firdes taps generating function.

Parameters

(R): Run-time adjustable

FIR Type

options: [Complex->Complex (Decimating), Complex->Complex (Interpolating), Float->Float (Decimating), Float->Float (Interpolating)]

Decimation or Interpolation

decimation or interpolation factor (depending on which type is chosen above).

Gain (R)

Overall gain of filter (default 1.0)

Sample Rate (R)

Sample rate in samples per second.

Symbol Rate (R)

The baud rate. The RRCF seems to work best setting this parameter to baud_rate * 2

Alpha (R)

Excess bandwidth factor, also known as alpha. (default: 0.35) With a very small alpha, say 0.001, the RRCF block produces sinusoidal-shaped symbols and culls more noise, whereas a large alpha produces more flat-topped symbols.

Num Taps (R)

Number of taps. This defaults to 11*samp_rate, but this default is not actually in the code and such a default produces extremely high CPU costs. If the number of samples per symbol is known, a better default would be working_sps * num_symbols which allows the filter to rolloff across num_symbols on either side. Its often handy to work with a small number of samples/symbol, say 8, and a reasonable rolloff for num_symbols may be 32, in which case Num Taps is quite small and thus the RRCF block consumes fewer CPU resources. Experiment with this number to find a useful range for the filter in your situation. Note that the number of generated filter coefficients will be num_taps + 1.

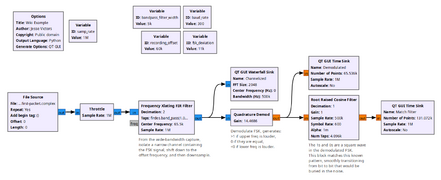
Example Flowgraph

Frequency-Shift Keying

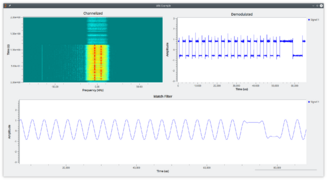
If you have demodulated Frequency-Shift Keying signal using a Quadrature Demod block, and you know the baud rate of the signal, and thus the duration of each symbol, the RRCS is useful for pulling these symbols out of the noise. In the process, the RRCS generates sinusoidal waves in place of the original square-wave symbols, rising from and falling to 0 and peaking at the center of each symbol. This result is extremely advantageous for clock recovery, as blocks like Symbol Sync need to lock onto the center of each symbol in order to reliably extract bits. The RRCS accomplishes both steps at once.

In the below example, the RRCF performs match filtering against a Frequency-Shift Keying signal. No noise has been introduced in this example; it just isolates the narrow channel containing the signal, demodulates it, and then performs match filtering. In this example, Symbol Rate is set to baud_rate * 2.

• 

  An example flowgraph of this block, demonstrating how the RRCF implements a match filter against the demodulated FSK signal.

• 

  The RRCF isolates the square-wave symbols and produces sinusoidal waves, peaking in the center of each symbol.

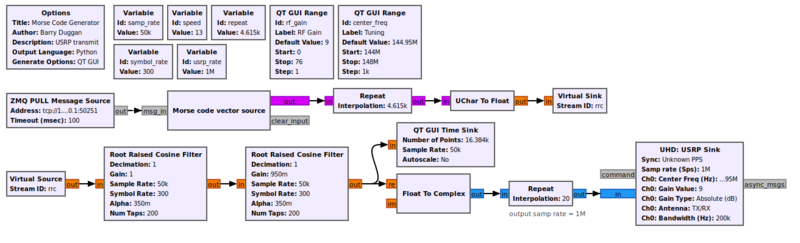
Waveform Shaping

This flowgraph can be found at [1]. Two Root Raised Cosine Filters in series produce a Raised Cosine Filter which is used for keying waveform shaping, thereby reducing key clicks.

Source Files

C++ files

[2]

Header files

TODO

Public header files

Taps creation

Filter definition

Block definition

[3]