Quadrature Demod: Difference between revisions
No edit summary |
(add Example Flowgraph) |
||
| Line 29: | Line 29: | ||
== Example Flowgraph == | == Example Flowgraph == | ||
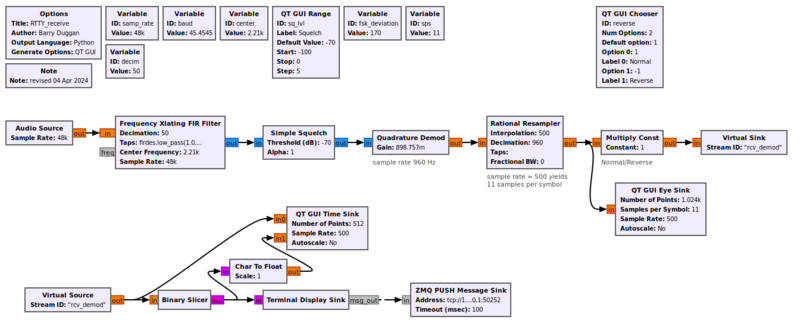
This flowgraph shows the Quadrature Demod block as a Frequency Shift Keying detector. | |||
[[File:RTTY_rcv.png|800px]] | |||
== Source Files == | == Source Files == | ||
Revision as of 13:10, 27 October 2019
This can be used to demod FM, FSK, GMSK, etc. The input is complex baseband, output is the signal frequency in relation to the sample rate, multiplied with the gain.
Mathematically, this block calculates the product of the one-sample delayed input and the conjugate undelayed signal, and then calculates the argument of the resulting complex number:
y[n] = \mathrm{arg}\left(x[n] \, \bar x [n-1]\right)
Let x be a complex sinusoid with amplitude A>0, (absolute) frequency f\in\mathbb R and phase \phi_0\in[0;2\pi] sampled at f_s>0 so, without loss of generality,
x[n]= A e^{j2\pi( \frac f{f_s} n + \phi_0)}\f
then
y[n] = \mathrm{arg}\left(A e^{j2\pi\left( \frac f{f_s} n + \phi_0\right)} \overline{A e^{j2\pi( \frac f{f_s} (n-1) + \phi_0)}}\right)\ = \mathrm{arg}\left(A^2 e^{j2\pi\left( \frac f{f_s} n + \phi_0\right)} e^{-j2\pi( \frac f{f_s} (n-1) + \phi_0)}\right)\ = \mathrm{arg}\left( A^2 e^{j2\pi\left( \frac f{f_s} n + \phi_0 - \frac f{f_s} (n-1) - \phi_0\right)}\right)\ = \mathrm{arg}\left( A^2 e^{j2\pi\left( \frac f{f_s} n - \frac f{f_s} (n-1)\right)}\right)\ = \mathrm{arg}\left( A^2 e^{j2\pi\left( \frac f{f_s} \left(n-(n-1)\right)\right)}\right)\ = \mathrm{arg}\left( A^2 e^{j2\pi \frac f{f_s}}\right) \intertext{$A$ is real, so is $A^2$ and hence only \textit{scales}, therefore $\mathrm{arg}(\cdot)$ is invariant:} = \mathrm{arg}\left(e^{j2\pi \frac f{f_s}}\right)\= \frac f{f_s}\\
A rendered version of the equations is available there: [1]
Parameters
- Gain
- Gain setting to adjust the output amplitude. Set based on converting the phase difference between samples to a nominal output value.
Example Flowgraph
This flowgraph shows the Quadrature Demod block as a Frequency Shift Keying detector.
Source Files
- C++ files
- [2]
- Header files
- [3]
- Public header files
- [4]
- Block definition
- [5]