Polyphase Arbitrary Resampler
Polyphase filterbank arbitrary resampler.
This takes in a signal stream and performs arbitrary resampling. The resampling rate can be any real number r. The resampling is done by constructing N filters where N is the interpolation rate. We then calculate D where D = floor(N/r).
Using N and D, we can perform rational resampling where N/D is a rational number close to the input rate r where we have N filters and we cycle through them as a polyphase filterbank with a stride of D so that i+1 = (i + D) % N.
To get the arbitrary rate, we want to interpolate between two points. For each value out, we take an output from the current filter, i, and the next filter i+1 and then linearly interpolate between the two based on the real resampling rate we want.
The linear interpolation only provides us with an approximation to the real sampling rate specified. The error is a quantization error between the two filters we used as our interpolation points. To this end, the number of filters, N, used determines the quantization error; the larger N, the smaller the noise. You can design for a specified noise floor by setting the filter size (parameters filter_size). The size defaults to 32 filters, which is about as good as most implementations need.
The trick with designing this filter is in how to specify the taps of the prototype filter. Like the PFB interpolator, the taps are specified using the interpolated filter rate. In this case, that rate is the input sample rate multiplied by the number of filters in the filterbank, which is also the interpolation rate. All other values should be relative to this rate.
For example, for a 32-filter arbitrary resampler and using the GNU Radio's firdes utility to build the filter, we build a low-pass filter with a sampling rate of fs, a 3-dB bandwidth of BW and a transition bandwidth of TB. We can also specify the out-of-band attenuation to use, ATT, and the filter window function (a Blackman-harris window in this case). The first input is the gain of the filter, which we specify here as the interpolation rate (32).
self._taps = filter.firdes.low_pass_2(32, 32*fs, BW, TB, attenuation_dB=ATT, window=filter.firdes.WIN_BLACKMAN_hARRIS)
The theory behind this block can be found in Chapter 7.5 of the following book:
f. harris, "Multirate Signal Processing for Communication Systems", Upper Saddle River, NJ: Prentice Hall, Inc. 2004.
Parameters
(R): Run-time adjustable
- Resampling Rate (R)
- Specifies the resampling rate to use
- Taps (R)
- (vector/list of floats) The prototype filter to populate the filterbank. The taps should be generated at the filter_size sampling rate.
- Number of Filters
- (unsigned int) The number of filters in the filter bank. This is directly related to quantization noise introduced during the resampling.
- Stop-band Attenuation
- This value is used to create taps.
- Sample Delay
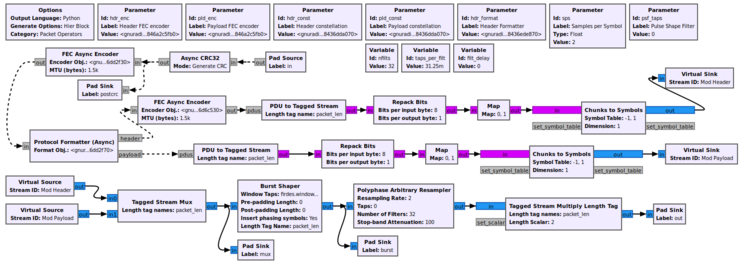
Example Flowgraph
This flowgraph can be found at [1]
Source Files
- Public header files
- Complex input and taps
- Complex input and float taps
- Float input and taps
- Base
- Block definition
- filter_pfb_arb_resampler.block.yml
See also
- Rational Resampler
- If you can represent the (output rate)/(input rate) fraction with small denominator and enumerator (e.g., (3.2 kHz)/(5 kHz)=16/25), this is both faster and usually better in signal quality